基本原理
 圖1
圖1Golomb編碼是一種分組編碼,需要一個正整數參數m,然後以m為單位對待編碼的數字進行分組,如圖1。
對於任一待編碼的非負正整數N,Golomb編碼將其分為兩個部分:所在組的編號GroupID以及分組後餘下的部分,GroupID實際是待編碼數字N和參數m的商,餘下的部分則是其商的餘數,具體計算如下 :
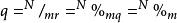 格倫布編碼
格倫布編碼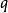 格倫布編碼
格倫布編碼對於得到的組號使用一元編碼(Unary code),餘下部分r則使用固定長度的二進制編碼(binary encoding)。
一元編碼(Unary coding)是一種簡單的只能對非負整數進行編碼的方法,對於任意非負整數num,它的一元編碼就是num個1後面緊跟著一個0。例如:
| num | Unary coding |
| 0 | 0 |
| 1 | 10 |
| 2 | 110 |
| 3 | 1110 |
| 4 | 11110 |
| 5 | 111110 |
例子
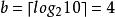 格倫布編碼
格倫布編碼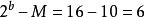 格倫布編碼
格倫布編碼設定M = 10。因此。截止值為。
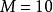 格倫布編碼
格倫布編碼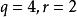 格倫布編碼
格倫布編碼例如,對於參數的Rice-Golomb編碼,十進制數42首先被分成並且將被編碼為qcode(q),rcode(r)= qcode(4),rcode(2)= 11110,010(你不需要對輸出流中的分隔逗號進行編碼,因為q代碼末尾的0足以說明當q結束並且r開始時; qcode都是 和rcode是自我分隔的)。
自適應遊程Golomb-Rice編碼
當未知整數的機率分布時,則無法確定Golomb-Rice編碼器的最佳參數。因此,在許多套用中,使用兩遍方法:首先,掃描數據塊以估計數據的機率密度函式(PDF)。然後根據估計的PDF確定Golomb-Rice參數。該方法的更簡單的變化是假設PDF屬於參數化族,從數據估計PDF參數,然後確定計算最佳Golomb-Rice參數。這是下面討論的大多數應用程式中使用的方法。
有效編碼其PDF未知或正在變化的整數數據的另一種方法是使用向後自適應編碼器。 Run-Length Golomb-Rice(RLGR)使用一種非常簡單的算法來實現,該算法根據最後編碼的符號向上或向下調整Golomb-Rice參數。解碼器可以遵循相同的規則來跟蹤編碼參數的變化,因此不需要傳輸任何輔助信息,只需要傳輸編碼數據。假設廣義高斯PDF覆蓋了數據中看到的各種統計數據,例如多媒體編解碼器中的預測誤差或變換係數,RLGR編碼算法可以在這樣的套用中很好地執行。
編解和解碼
其編解和解碼的偽代碼如下:
