目錄：
1.古希臘早期的宇宙觀與天文學理論
2.歐多克索的同心球模型
3. “兩球宇宙”模型的缺陷
4. “本輪-均輪”模型的提出與初步完善
5. 托勒密對“本輪-均輪”體系的發展
6. 哥白尼體系下的“本輪-均輪”模型
7. 第谷的“折中宇宙”中的“本輪-均輪”模型
8. 被遺棄的“本輪-均輪”模型
1.古希臘早期的宇宙觀與天文學理
古希臘的地域範圍於今天的希臘有所不同，古希臘不僅包括了今天的希臘領土，還應當包括今天的義大利南部，土耳其西部及其他一些地區。古希臘位於歐洲南端，主要領土希臘半島、愛琴海諸島嶼、愛奧尼亞群島、西西里島等均處在地中海周邊地區，地理特徵、氣候條件較為接近。古希臘地形崎嶇，有大量的狹窄山谷、細長的海灣、河流很少而海島較多，是典型的地中海氣候區。
由於古希臘土地貧瘠、糧食短缺而人口眾多等特點，使得古希臘不得不通過開展海外殖民活動和大量的對外貿易來解決這些危機。由於古希臘島嶼眾多，相互之間的聯繫也需要通過海路來實現。海外貿易、戰爭的人員、物資運送也使得古希臘的海運事業極其發達。由於航運事業的需要，古希臘人積累了足夠的關於大地測量學等知識，海洋航運需要靠觀察天象來指引方向，通過商業途徑和古巴比倫人和埃及人的交流也對他們的天文學體系的形成獲益匪淺。古希臘人由此對 “行星有序運動的原因”，“宇宙的本源”等問題展開了討論。
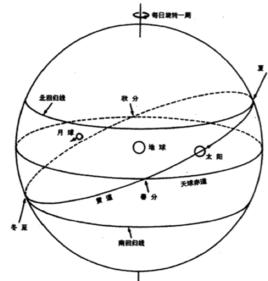
古希臘哲學家泰勒斯首先從埃及引入大地測量術，並發展了幾何學，還提出了“水”是萬物本源的說法。他的學生阿那克西曼德提出宇宙是球形的，星辰鑲嵌在球形之上。阿那克西曼德的學生阿那克西米尼改進了這個宇宙模型，認為宇宙是個半球，罩在大地之上，而大地則像是一個盤子漂浮在氣上。還有許多人對宇宙的本源和形狀都提出了猜測和推斷，這些推斷都對以後古希臘天文學的發展多多少少起到了促進作用。值得一提的是古希臘的畢達哥拉斯學派把世界的本源歸結為“數”。對於畢達哥拉斯學派來說，宇宙是一個完美、有序以及和諧的統一體，而數字和數學關係則決定了這種完美與和諧。在他們看來，世間事物的關係都可以用數字來表示。他們還認為，在所有的幾何圖形中，只有球和圓是最完美與和諧的形體，因為它們圓轉無缺、無始無終、可以自轉而不移動，只有他們才適合用來表現宇宙的完美與和諧。因此宇宙及其中的日月星辰都是球形，它們的運動都是勻速圓周運動或其組合。這種觀念由此成為西方天文學家和宇宙學史上的一個核心理念，直到近代的歐洲還被天文學家認為是“天文學公理”，直到克卜勒時代才被打破。
著名哲學家柏拉圖也深受畢達哥拉斯學派的影響，他也將物質性本源的世界歸結為數學性的實體。他在《理想國》中談到了要加強對立體幾何的研究，而且已經知道了正多面體只有五種。柏拉圖還建立了一個幾何宇宙模型，在這個模型中，地球日月星辰都是球形，都做圓周運動。不過地球處在宇宙中心，恆星所在的天球是宇宙的邊界，在它和地球之間，是月亮、太陽和五大行星繞地球運行的圓圈，半徑滿足1：2：3：4：8：9：27的比例關係。日月五星參與兩種運動，一方面隨著天球每日一周，另一方面又在各自的圓圈上一部通俗動運動。五顆行星的周期不同，有時候會出現逆行的現象。在柏拉圖時期，許多天文學的“傳統”已然確立下來，這對後世的天文學研究起到了框定和示範的作用。 在商務印書館出版的最新版的《天球運行論》的序言中，吳國盛將柏拉圖時期確立下來的宇宙論的六個基本要點總結如下：
（1）宇宙是球形（層層相套的諸天球的組合）；
（2）諸天體均鑲在各自的天球上隨天球運動；
（3）天球的運動是均勻的圓周運動；
（4）大地是球形的；
（5）地球絕對靜止；
（6）地球居於宇宙的幾何中心（托勒密對地球不處於宇宙中心三個位置的論證）。
以上這些理念深深地影響到了後來的天文學家，在阿里斯塔克《論日月的大小及距離》和托勒密的《至大論》中都有部分體現和繼承。此外，關於天求究竟是一種真實存在的物理實體，還是一種用以描述天體運動的數學工具？這個問題引發了“拯救現象”的傳統。即“通過什麼樣的勻速有序的運動，才能夠解釋行星表觀運動？”。這一傳統奠定了古希臘天文的另一個基調，為了回答這個問題，遵循這個傳統，古希臘的後代天文學家付出了巨大的努力。我們可以看到，在這個階段古希臘天文學形成了自己的天文學傳統，形成比較完整的宇宙觀和關於天文學理論的研究方法。在以後的天文學理論中，我們也會看到這些人的工作對於後代天文學家的影響。
2.歐多克索的同心球模型
本輪均輪系統前面講到了古希臘的“拯救現象”傳統，為了用勻速圓周運動來解釋人們在地球上觀察到的行星運動的情況，產生了許多天文學模型和理論。這些模型基本都在原有的古希臘宇宙論傳統和畢達哥拉斯派的數學與幾何理論下進行的。但是當時以柏拉圖等人為代表的宇宙模型存在明顯的缺陷，不能對一些觀察到的現象進行較好的解釋。主要是太陽、月亮、恆星、星座會出現規律的整體移動，但是金、木、水、火、土會出現不太規則的運動。比如在午夜觀測火星的時候會發現它出現逆行、停留、順行的現象。為了解決這些問題，柏拉圖的學生歐多克索提出了第一個有意義的模型—同心球宇宙模型。
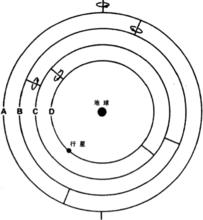
如右圖所示，歐多克索的同心球宇宙模型中將地球固定在天球的中心，天球繞垂直的軸自轉。天球是一個透明的水晶球殼層，各行星附著在天球的表面做各種運動。地球的赤道也就是天球的赤道面，黃道面也是如此。太陽、月球和行星走黃道，太陽月球運動速度幾乎不變，其他的行星運行的方向也不變但是速度差異很大。
本輪均輪系統歐多克索發現，用3個球就可以複製出日月的運動，行星的運動則要用4個球。五大行星加上日月和恆星天，一共需要27個球。通過適當的選取這些球的旋轉軸，旋轉速度和球半徑就可以是這套天求系統比較準確的再現當時所觀測到的天體運動情況。
在當時的條件看來，這套模型具有不少創新之處，大致上也能夠符合觀測到的一些現象。總而言之是不小的進步，對之後的天文學理論起到了不少參考作用。歐多克索的學生卡利普在原有的27個天球的基礎上再增加了7個天球，以獲得與天文觀測更精確相符的結果。亞里士多德則是在卡利普的基礎上把同心球宇宙模型改造為一個可以自圓其說的宇宙體系，在亞里士多德看來 , 天球是真實的物理實體，是由透明而又無重量的以太構成的固體球。諸天球共同構成一個機械聯動裝置，在最外層天球的帶動下一起運動。為了實現諸天球的聯動 ，亞里士多德的宇宙模型比卡里普斯的多了22個天球。
3. “兩球宇宙”模型的缺陷
歐多克索等人確立的同心球模型中，地球是靜止的懸在一個更大球體幾何中心的小球，這個更大的球體攜帶恆星並且在轉動。太陽在地球和恆星天球之間廣大的空間之中運動。托馬斯·庫恩將這個模型稱之為“兩球宇宙”模型。
即便同心球模型得到了很好的繼承和發展，但是它仍舊存在一些重大的缺陷。首先，每個行星都被放置在以地球為中心的天球上，所以這些“行星”與地球的距離保持不變，但是實際上的觀測卻發現地球與其他行星的距離是有變化的。特別是當某些行星逆行時，按照同心球模型他的亮度應該是要降低的，但是實際上卻變得更亮了。此外，同心球模型也沒有辦法解釋“停、留”的現象。最後，如果太陽繞地球做勻速圓周運動，那么一年中四個季節的天數是不相等的。
以上這幾個問題對於同心球模型提出了嚴峻的挑戰，由於模型本身的缺陷，雖然不斷有人對其發展和改進，這些問題仍然沒有很好地解決。雖然如此，之後的天文學家也是在其基礎上不斷調整模型，並沒有完全跳出“兩球宇宙”模型。“本輪—均輪”體系就是為了解決同心球模型的諸多問題而提出來的一種新的幾何模型。但是這種幾何模型仍然是在同心球模型的體系下進行的，只不過採用了全新的勻速圓周運動的疊加而已。
4. “本輪-均輪”模型的提出與初步完善
本輪均輪系統根據托勒密《至大論》的記載，阿波羅尼烏斯最早發明了“本輪—均輪”模型，而這個模型最早是由希帕克斯繼承使用。這個模型著眼於解決同心球模型面臨的幾大無法解釋的觀測現象而進行。
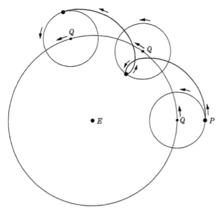
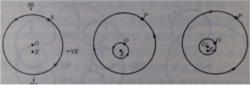
如圖所示，在本輪-均輪模型中，地球位於E點，地球所在的大圓是均輪（deferent），均輪的本身以一定的速度勻速旋轉。而行星P所在的小圓是本輪（Epicycle），Q是本輪的圓心。本輪-均輪的旋轉總和使得行星看起來會向後退、停留等現象。對於每一個行星都設計一個“本輪-均輪”體系，太陽和月亮不會出現逆行，所以只需要一個均輪即可。通過改變本輪和均輪的相對大小、相對速度，該合成的圓周組合可以很好地定性的解釋行星的不規則運動，當行星運行到最接近地球時，即會發生逆行，且在此位置上行星看起來最明亮。
與此同時，阿波羅尼烏斯還提出了另一種模型—偏心圓模型—來表征天體的運行規律。如圖所示，行星P在圓周上相對於圓心O做勻速圓周運動，地球則處於偏離O的一點T上。這樣從地球上看來，行星的距離和相對地球的速度都會發生變化。一定條件下，偏心圓模型和本輪-均輪模型等價，但是只有本輪-均輪模型可以描述停留和逆行現象。
本輪均輪系統阿波羅尼烏斯之後的希帕克斯，發明了和現代正弦函式等效的函式方法，並且基於原有的“本輪-均輪”模型和偏心圓模型、長期的觀測數據，建立了比較完善的太陽和月亮的運動理論。據說可以實現對日月位置計算的同時，還能夠基本準確的預報日食和月食。
此外，他還根據古巴比倫的觀測資料，發現了赤道年（太陽回到春分點）比恆星年（太陽回到同一恆星）略短一點，由此發現了歲差。他還提出這是因為春分點會繞著與黃道面垂直的軸作微小的進動。這個發現對完善同心球模型也有一定的幫助。
阿波羅尼烏斯和希帕克斯的工作至關重要，不過在希帕克斯之後的300多年間，天文學家尚未能利用“本輪—均輪”模型和偏心圓模型構造出能夠定量描述行星運動的體系。 對於行星運動的規律仍舊處在一個粗略的定性觀察的觀察階段，而基於這些模型的更加精密準確的定量計算則是在另一位天文學家出現之後才得到了解決。
5.托勒密對“本輪-均輪”體系的發展
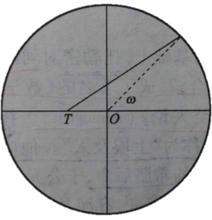
在阿波羅尼烏斯和希帕克斯的基礎上，托勒密獨創了 equant（偏心勻速圓）模型。傳統的“本輪—均輪”模型是讓地球處於圓心O，這種模型的優點前文已經講過。但是在Equant 模型中地球位於點E處，本輪的中心C仍然在以O為中心的均輪上轉動，但是它相對圓心O來說並不是勻速圓周運動，而是相對於“Equant”點E’的勻速角運動。
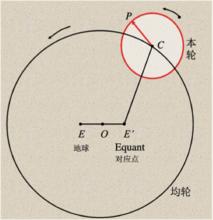本輪均輪系統吳國盛專門討論過equant模型中“equant”一詞的譯法，目前對equant的翻譯有：對稱點、偏心等距點、等分圓、對分圓、對點、均衡點、偏心勻速點、等分點等等。為了避免出現混亂，我們統一採用“偏心勻速點”的譯法。對於托勒密體系，不少人給與了極高的評價。石雲里認為托勒密的“等分點模型”是“古代最接近橢圓軌道理論的模型”。
庫恩在《哥白尼革命》（P64）中說道：“它的所有繼承者包括哥白尼在內都是模仿他來開展工作”。托勒密的體系從出現以來被他的繼承者們多次修正，不同版本的托勒密天文學採用的小本輪的數量相差很大，在中世紀和文藝復興時使用6到12個小本輪不少見，通過對小本輪的尺寸和速度的適當選擇，幾乎所有微小的不規則性都可以解決。“這就是哥白尼體系其實和托勒密體系幾乎一樣複雜的原因，儘管哥白尼消除了大本輪，但是他仍然和他的前輩一樣依賴小本輪”。
“本輪—均輪方法因為設計精巧，適應性強，結構複雜，功能強大，在科學史上直至近代之前一直無出其右。在它最發達的形態中，組合預案體系是一項令人驚嘆的成就。但是它從來沒有完全解決問題”。實際上，“托勒密體系有許多變種以至於可以十分精確的預測行星位置，但是這種精確性的獲得是以複雜為代價—增添新的本輪或相當的裝置—而不斷增加的複雜性只能為行星運動提供更好的近似，而不能最終解決。體系的任何一種形式都沒能徹底經受住更精確的觀測的檢驗，這種失敗加上概念經濟型總體上的消失最終導致了哥白尼革命，而這種經濟性曾經使粗糙的兩球宇宙都能讓人信服”。
本輪均輪系統 本輪均輪系統如圖是均輪之上的本輪之上的本輪的組合，當均輪旋轉一周，大本輪向東八周而小本輪向西一圈，那么行星在恆星天球上描出的路勁就如同右圖所示，如果小本輪速度加快一倍，這是的路徑就是一個橢圓。在體系中增加偏心圓的偏移圓和增加小本輪是等價的，通過將偏心圓的圓心放在一個小的均輪上或放在次一級更小的偏心圓上，就可以得到額外的效果。對於一個均輪上的小本輪和下一級偏心圓上的小本輪來說，這兩種方法在幾何上來說是完全等價的。
6. 哥白尼體系下的“本輪-均輪”模型
哥白尼在《天球運行論》中首先是規定了我們熟知的地球的三重運動：自轉，繞日公轉，傾角的轉動。同時他還指出與恆星天球相比，日地距離可以忽略不計。這時如果把周年轉動從太陽換到地球而把太陽視為靜止，那么黃道各宮和恆星在清晨和傍晚都會顯現出同樣的東升西落；而且行星的留、逆行、順行都可以認為不是行星的自行，而是地球運動的反映。
在哥白尼的體系中，地球是鑲嵌在天球上繞太陽公轉的，並且地球本身也有自轉。星空的變化實際上是由於地球的自轉造成的，地球的自轉引起了晝夜的變化，而太陽的周年視運動則是由於地球繞太陽公轉造成的。此外，哥白尼用太陽取代地球成為宇宙的中心，所有的行星包括地球均以太陽為中心轉動。但是哥白尼也強調相比於宇宙天球的大小，地球與太陽之間的距離可以忽略。
哥白尼的體系中，大小輪子的數量大大減小了，所有的輪子都朝一個方向運動，偏心勻速點也被取消了。相較而言，哥白尼體系沒有藉助本輪至少是大本輪就對行星運動做出了同樣的定性解釋。對於只考慮行星定性運動的天文學家來說，哥白尼的體系肯定經濟的多。但是在作出定量解釋的時候，哥白尼也需要求助於小本輪和偏心圓。在這個意義上，哥白尼體系和托勒密體系的準確度和經濟性其實差不多，實際上也沒有解決問題。
7. 第谷的“折中宇宙”中的“本輪-均輪”模型
第谷的“折中宇宙”模型是作為對哥白尼體系所導致問題的折中方案，對聖經，恆星視察，運動定律之間都得到了調和，而且沒有犧牲哥白尼的數學和諧型。
本輪均輪系統如下圖所示，是第谷體系的示意圖。像托勒密體系一樣，太陽、月亮和行星都在最外層天球的帶動下向西運動。地球處於旋轉的恆星天球的中心，月亮太陽的圓圈以地球為中心，但是剩下五顆行星的中心則是從地球變成了太陽。在這個體系中，小本輪、偏心圓和偏心勻速圓也是必須的。
值得一提的是，第谷體系雖然和哥白尼體系在數學上是等價的，但是第谷有更精確的觀測資料作為支撐，為曆法改革奠定了基礎。在他的觀測基礎之上，1582年，教皇格里高利十三世對沿用了一千多年的儒略曆做出了改革，頒布了格里高利曆。
8. 被遺棄的“本輪-均輪”模型
我們看到，即便是在對傳統的天球模型有極大改動的哥白尼體系和第谷體系中，“本輪—均輪”模型仍然發揮著它的作用。如果說哥白尼是“古代最後一位天文學家”那么克卜勒就是真正意義上的“現代第一位天文學家”。克卜勒在第谷的大量的觀測資料的基礎上，經過大量的計算和嘗試得到了“克卜勒三大定律”。
通過克卜勒的三大定律—面積、軌道、周期定律，徹底打破了以勻速圓周運動為基礎的“天文學公理”。使得傳統的天球觀念難以為繼，也徹底的顛覆了沿用約2000年的“本輪-均輪”模型。
參考：
董雯雯. 希臘民主政治研究[D]. 遼寧師範大學, 2013.
吳國盛. 科學的歷程[M]. 湖南科學技術出版社, 2013.
石雲里. 科學簡史[M]. 首都經濟貿易大學出版社, 2010.
哥白尼[波蘭]. 天球運行論[M]. 商務印書館, 2014.
吳國盛. 是“天球”不是“天體”——紀念哥白尼《天球運行論》出版460周年[J]. 自然辯證法通訊, 2003, 25(6):98-101.
李巍. 比較《周髀算經》與阿利斯塔克《論日月的大小和距離》的公理化方法[J]. 青年與社會, 2013(9):221-223.
鄧可卉. 希臘數理天文學溯源[M]. 山東教育出版社, 2009.
項武義. 千古之謎與幾何天文物理兩千年[M]. 高等教育出版社, 2010.
庫恩. 哥白尼革命[M]. 北京大學出版社, 2003.
鄧可卉. 托勒密《至大論》研究[D]. 西北大學, 2005.
吳國盛. Equant譯名芻議[J]. 自然辯證法通訊, 2007, 29(1):92-95.
鈕衛星. 天文學史[M]. 上海交通大學出版社, 2011.
伏古勒爾. 天文學簡史[M]. 上海科學技術出版社, 1959.
吳光節. 從科普插圖看托勒密的地心說[J]. 天文研究與技術, 2015(3):381-384.
鄭偉. 天文學基礎[M]. 國防工業出版社, 2006.
