概念
朗伯四角形(Lambert quadrangle)是歷史上用以研究第五公設問題的四邊形。德國數學家朗伯(Lambert，J.H.)在1766年發表的《平行線》中，有類似於義大利數學家薩凱里(Saccheri，G.)的研究。朗伯從討論四角形ABCD出發(如圖)，在這個四角形中，有三個內角被假定為直角，即：
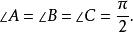朗伯四角形人們把這個四角形稱為朗伯四角形，而把那個沒有假定為直角的內角稱為朗伯角，並記為L ，即∠D=L 。對於L ，有且僅有：
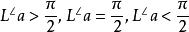朗伯四角形三種情形。而“L=π/2”等價於第五公設，並且若設L>π/2，則立即導致矛盾。從而，朗伯也只要不以第五公設為基礎而能否定L<π/2，就能完成第五公設的證明。這樣，朗伯從假定L<π/2出發，希望在不以第五公設為基礎的前提下導致矛盾，從而達到否定L<π/2之目的。然而在這個前提下，不論如何深入地進行推導和演繹，始終未能引出兩個在邏輯上互相排斥的命題。
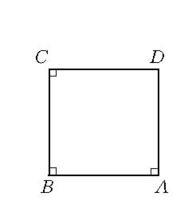圖1郎伯四角形應當指出，在當時，朗伯的幾何觀點是最先進的，工作也推進得最遠，他不僅從來沒有聲稱過自己已經證明了第五公設，而且“他認識到，任何一組假設如果不導致矛盾的話，一定能提供一種可能的幾何，這種幾何是一種真的邏輯結構，雖然它或許對真實的圖形作用很少，後者或可提示一種特別的幾何，但不能限制邏輯上可能發展千差萬別的幾何。”在這裡，L=π/2也僅僅是第五公設的一個等價命題。
第五公設問題
由關於歐氏幾何中第五公設的爭議而形成的一個問題。883年到1889年，《幾何原本》的版本是經過科學地整理而翻印的，從而被公認為標準版本。此版本的第一卷開端有23個定義，然後引進公設和公理。其中第五公設的內容是：若兩直線與第三條直線相交，其一側的兩個內角之和小於兩直角時，則把這兩條直線向著該側充分地延長後一定相交。第五公設的陳述和內容與其他公設或公理相比較，顯得複雜和累贅，顯然沒有其他公設、公理那樣自明。所以古代學者們早就懷疑，第五公設能否從其他公設、公理中推導出來?這就是所謂第五公設問題。
古代學者還進一步認為，歐幾里得(Euclid)之所以把第五公設當做公設，乃是因為他未能給出這一命題的證明，從而也將這一點視為《幾何原本》體系中的一個重要缺點。繼而學者們付出了巨大的精力去證明第五公設。幾乎可以說在歐幾里得以後的兩千多年時間裡，難以發現一個沒有試證過第五公設的數學家。但是，所有試證第五公設的努力都失敗了，在所有這些失敗的證明中，或是最終發現某些證明步驟有誤，或是發現在證明過程中暗自使用了與第五公設等價的命題.例如，“三角形三內角之和等於π”就是人們最熟知的與第五公設等價的命題之一.但是，在假定實數系統R無矛盾的前提下卻可以明確回答這個問題。龐加萊模型和笛卡兒模型的構造成功表明了，在實數系統R無矛盾的前提下，歐幾里得與羅巴切夫斯基幾何公理系統都是無矛盾的(參見“龐加萊模型”、“笛卡兒模型”).因此，可以斷言歐氏平行公理不可能在絕對幾何公理系統中被推演出來.否則，若設歐氏平行公理是絕對幾何系統中的一個命題的話，那么歐氏平行公理與羅氏公設這樣兩個互相矛盾的論斷就要在羅巴切夫斯基幾何公理系統中並存，從而羅氏幾何公理系統就成為一個不相容的系統。同理可知，由歐幾里得幾何公理系統的相容性可以證明羅氏公設也不是絕對幾何公理系統中的命題。
朗伯
德國數學家。生於阿爾薩斯(Alsace)，是一家成衣商之子，家景貧寒，求學時是工讀學生，曾當過會計、家庭教師。1763年前往柏林科學院任職，晚年任俄國航海曆編譯長。死於柏林。
朗伯是歐拉(Euler，L.)和拉格朗日(Lagrange，J.-L.)在柏林科學院的同事，雙曲線三角法的創立者。主要著作有《光學》和《透視學》(1759)、《彗星論》(1761)；重要論文有：《關於超然量》(1768)，證明了π和e為不可通約量；《關於三角法》(1768)，詳述了棣莫弗定理，而以cos hx、sin hx之記號代表雙曲線正餘弦等。他對平行線理論的研究也很深入。在天文學方面，他提出關於星系的假說。此外，他對哲學也有一定研究。
