移動自組網路分散式組密鑰更新算法
安全性是移動自組網路組通信的基本需求,安全、高效的組密鑰更新算法是保證組通信安全的關鍵。在移動自組網路分散式組密鑰管理框架(distributed group key management framework,簡稱DGKMF)的基礎上,提出了一種組密鑰更新算法——DGR(distributed group rekeying)算法。該算法能夠利用局部密鑰信息更新組密鑰,適合拓撲結構變化頻繁、連線短暫、頻寬有限的移動自組網路。為了進一步降低算法的通信代價,通過在組密鑰更新時動態生成組密鑰更新簇,對DGR算法進行了改進,提出了CDGR(cluster distributed group rekeying)算法,並討論了上述算法的安全性、正確性和完備性,分析了算法的通信代價。最後,利用ns2模擬器對算法的性能進行了分析。模擬結果顯示,DGR和CDGR算法在組密鑰更新成功率和延遲等方面均優於其他算法,並且由於採用簇結構,CDGR算法的更新延遲低於DGR算法。
TEK更新算法
在組通信過程中,數據的私密性通過TEK加密實現.當節點加入或退出時,組成員節點都需要更新TEK,以保證通信的後向私密性和前向私密性。
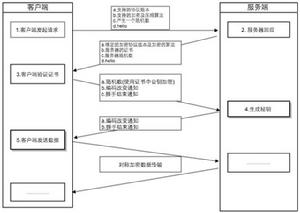
在DGKMF中,請求加入的組成員需要由離線組控制節點或門限個組成員節點為其頒發組成員資格證書。利用TEK更新算法,新加入的組成員與其鄰居節點生成新的組密鑰以後,用已有的組密鑰加密新的組密鑰,向組中所有節點廣播,以更新組密鑰。
組成員退出分為主動退出和強制退出兩種情況。當組成員主動退出時,它向全組廣播退出請求。強制退出請求由發現異常的節點廣播。接到退出請求的組成員利用TEK更新算法更新組通信密鑰,同時將退出組成員的資格證書加入到證書廢除列表中,以防止已退出的組成員參與密鑰更新過程。
高效、安全的組密鑰更新算法對於安全組通信至關重要。在DGKMF的基礎上,提出了兩種組密鑰更新算法:DGR算法和CDGR算法.這兩種算法均只需利用局部密鑰信息更新組密鑰,避免了移動自組網路拓撲結構變化頻繁、連線短暫等特點對組密鑰更新的影響;其主要區別在於密鑰更新的方式不同。在DGR算法中,每個節點均需要與門限個以上的鄰居節點通信,以更新組密鑰,局部通信代價較大。而CDGR算法在組密鑰更新時動態生成組密鑰更新簇,通過建立層次結構降低了組密鑰更新的通信代價。
假設節點在密鑰更新過程中時鐘同步,節點在更新過程中安全可靠,且節點通信具有鬆散的同步機制支持。
模擬實驗
在實際環境下,移動自組網路的連通性以及鏈路的可靠性難以保證.因此,為了驗證算法的有效性,採用ns2網路模擬器比較了DGR算法和CDGR算法在節點加入、退出時TEK更新的成功率和更新延遲,並比較了它與組密鑰管理協定CKD,GDH v2以及BD協定的性能。
模擬環境的鏈路可靠性為90%,節點的平均速度為10m/s,節點停等時間為5s.網路規模以節點數量表征,節要點數量是30~100,幅度10均勻變化。模擬空間隨網路節點數量變化,以保證網路的連通性,協定模擬時間為1500s。
由於組密鑰更新算法的性能與網路中節點的密度有密切的關係,將網路中組成員的平均鄰居數量稱為網路的連通強度,用D標識.當模擬時,D=5,即平均每個節點的鄰居數量為5。
根據網路連通強度為5,網路中節點的數量分別為30,40, … ,100,鏈路可靠性為90%,節點的最大移動速度為5m/s,節點停等時間為5s.的模擬實驗結果可以看出,DGR算法和CDGR算法依賴於局部通信更新組密鑰,延遲在30s 左右,隨著網路規模的擴大略有提高。由於組成員加入時,DGR,CDGR算法的密鑰更新過程類似,均需要為新加入的節點分發共享密鑰,因此算法的性能相當.在節點退出時,CDGR算法由於在組密鑰更新時動態生成更新簇,利用簇首節點局部生成並分發組密鑰,減少了本地通信代價,因此CDGR算法的延遲低於DGR算法.在節點加入、退出時,DGR算法和CDGR算法的TEK更新成功率均接近於100%。在相同的模擬條件下,CKD,GDH v2以及BD等組密鑰管理協定和算法的更新延遲平均在80s左右,組密鑰更新的成功率均低於90%,並且隨著組的規模增加性能急劇下降。其密鑰更新成功率和延遲均比DGR算法和CDGR算法要差。
MapReduce的並行關聯規則增量更新算法
為解決傳統關聯規則挖掘算法在大數據環境下運行效率較低的問題,基於頻繁模式增長(FP-growth)算法,提出一種面向大數據的並行關聯規則增量更新算法。利用MapReduce編程模型與雲計算平台,對FP-growth算法各步驟進行並行化處理。在增量更新挖掘過程中,使用已有的頻繁項集和1-項集對新增事務集構建頻繁模式樹,通過掃描原始事務資料庫完成頻繁項集的更新。實驗結果表明,與傳統關聯規則挖掘算法相比,該算法具有更高的挖掘效率和擴展性,適用於大量數據的關聯規則增量挖掘。
算法描述
PFP-growth算法是公認的高效並行關聯規則挖掘算法,該算法基於FP-growth算法,採用MapReduce編程模型,對FP-growth算法各個步驟進行並行化處理。在面對大量數據時,PFP-growth算法具有較高的準確性和伸縮性,解決了FP-growth算法單機情況下面對大量數據時性能不足的問題。但由於事務資料庫處於不斷更新中,PFP-growth算法仍然不能利用已有挖掘結果進行增量挖掘。主要是針對關聯規則的增量更新問題,提出並行關聯規則增量更新算法,該算法分為2個步驟:
(1)針對原事務資料庫DB進行分組,構建各映射資料庫,利用MapReduce並行挖掘出頻繁項集並保存,該步驟與PFP-growth算法類似;
( 2) 針對新增資料庫,利用之前的挖掘結果再次進行並行挖掘,完成頻繁項集的更新。
雲計算平台下的算法性能分析
實驗運行在Hadoop平台上,使用多檔案輸出功能以及Mahout工具實現了多個MapReduce任務的疊代運行。Hadoop平台由6個節點組成,其中,1台為Master節點; 其他5台為Slave節點。每個節點的硬體配置與單機情況下的實驗相同,作業系統為Ubuntu12.0.4,Hadoop版本為Hadoop-0.20.2,jdk版本為jdk1.7.0_45。實驗使用的數據集為webdocs.dat,webdocs.dat,數據大小為1.37GB,共有1692082條記錄,包含5267656個不同的項,其中,最長的事務有71472項。
實驗中首先將數據分為5組,選取數據集的20%作為原資料庫,記做data0,每次遞增20%進行並行增量挖掘,分別記做data1,data2,data3,data4,支持度為5%。將並行化算法與Mahout開源平台所提供的PFP-growth算法、文獻中的MRFUP算法進行比較,其中,算法和PFP-growth算法中的分組數均為5。
由Hadoop平台下的算法性能對比可以看出,相比PFP-growth算法,並行化算法很大程度上提高了挖掘效率,這是因為算法每次只對新增資料庫的分組構建條件FP-tree,節約了每個分組構建FP-tree的時間。MRFUP算法雖然也是基於MapReduce的增量更新算法,但是算法的很多步驟仍然是在單機環境下,只有對候選集的篩選是在雲計算平台下進行,因此,在數據量較大的情況下算法效率提高有限。隨著數據的不斷增加,並行化算法的時間開銷增幅平穩,在大數據環境下能保持穩定。因此,實驗結果證明了並行化算法適用於大數據環境下的增量更新。
為了驗證算法的可擴展性,將數據集的80%作為原資料庫,20%作為新增資料庫,支持度分別設為5% ,10%和15% ,分別基於1個~5個Slave節點比較算法的運行時間,由不同Slave節點和支持度下的算法運行時間對比可以看出,在數據和支持度相同的情況下,隨著Slave節點數量的增加,算法執行時間逐漸降低,這是因為Hadoop集群具有高度並行性,而在一個機架內節點之間的通信開銷較小,從而程式整體運行時間不斷減少。而在數據和節點相同的情況下,當支持度較大時,運行時間較少,這是因為隨著支持度增加,數據的頭表中的項目變少,分發數據和建立FP-tree的時間開銷都會降低。