背景
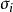 易辛模型
易辛模型 易辛模型( Ising model,(/ˈaɪsɪŋ/;德語:[ˈiːzɪŋ]),是一個以物理學家恩斯特·易辛為名的數學模型,用於描述物質的鐵磁性。該模型中包含了可以用來描述單個原子磁矩的參數 ,其值只能為+1或-1,分別代表自旋向上或向下,這些磁矩通常會按照某種規則排列,形成晶格,並且在模型中會引入特定互動作用的參數,使得相鄰的自旋互相影響。雖然該模型相對於物理現實是一個相當簡化的模型,但它卻和鐵磁性物質一樣會產生相變。事實上,一個二維的方晶格易辛模型是已知最簡單而會產生相變的物理系統。
易辛模型最早是由物理學家威廉·冷次(Wilhelm Lenz, 1888-1957)在1920年發明的,他把該模型當成是一個給他學生恩斯特·易辛的問題。易辛在他一篇1924年的論文中求得了一維易辛模型的解析解,並且證明它不會產生相變。二維方晶格易辛模型相對於一維的難出許多,因此其解析的描述在一段時間之後才在1943年由拉斯·昂薩格給出。一般來說,二維易辛模型的解析解可由傳遞矩陣法求得,不過也有幾個和量子場論有關的解法。對於大於三維的易辛模型目前還沒有找到解析解,但其近似解可由諸多方法求得,例如平均場論。
定義
令Λ為所有晶格點的集合,其中每個晶格點都有一個所有和它相鄰的晶格點的集合(在數學上稱之為圖)並使這些晶格點形成一個d維的晶格。對於每個晶格點 k∈Λ 都有一個離散變數σ,其中 σ∈ {+1, −1},代表一個晶格點的自旋。而所有變數的集合σ=(σ)則稱作 自旋組態。
對於兩個相鄰的晶格點 i, j∈ Λ ,我們可以引入一個互動作用參數 J,此外,我們可以假設每個自旋 j∈Λ都和外加的磁場h作用。則整個系統的哈密頓量可寫成:
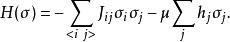 易辛模型
易辛模型 其中代表晶格點 i和晶格點 j是相鄰的的晶格點。因此哈密頓量的第一項為對每一對相鄰晶格點的總和(每一對只算一次),代表所有自旋之間互動作用的能量,而第二項則是磁場和自旋互動作用的能量。µ是晶格點磁矩的值,值得注意的是,電子的磁矩和他的自旋方向相反,所以哈密頓量的第二項應該要是正號比較合理,但在習慣上,還是會令第二項為負號。
該系統的的 組態機率P(σ)為在熱平衡下某個特定自旋組態 σ 的機率,為波茲曼分布:
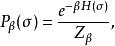 易辛模型
易辛模型 其中 β=( kT),而:
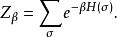 易辛模型
易辛模型 是該機率分布的歸一化常數,在統計力學中又稱做配分函式。對於有為自旋組態函式的物理量f(σ) ,其期望值可表示為:
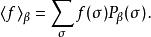 易辛模型
易辛模型 參數
H(σ) 中兩項前的負號是約定俗成的。因為第一項為負號,因此參數 J的正負號決定了該系統的性質,對於每一對 i和 j:
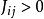 易辛模型
易辛模型 ,則該系統為鐵磁性。
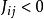 易辛模型
易辛模型 ,則該系統為反鐵磁性。
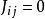 易辛模型
易辛模型 表示自旋間無互動作用。
除此之外該系統為 非鐵磁性。
在鐵磁性的易辛模型中,相鄰自旋同方向時能量較低,因此自旋會傾向於同向排列,反之,在反鐵磁性的易辛模型中,的相鄰自旋反向的能量較低,因此自旋會頃向於反向排列。
H(σ) 中的第二項為負號,表示自旋頃向於和外加磁場同向,因此 h的正負也決定自旋頃向排列的方向。對於所有的j ,如果:
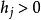 易辛模型
易辛模型 , 則晶格點 j頃向於朝向正向。
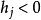 易辛模型
易辛模型 , 則晶格點 j頃向於朝向負向。
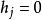 易辛模型
易辛模型 , 表示沒有外加力場作用在自旋上 。
簡化
一個常見的簡化是假設沒有外加的磁場作用在易辛模型上,也就是說,對於所有的 j∈Λ, h=0 。利用這項簡化,其哈密頓量可以寫成:
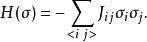 易辛模型
易辛模型 此時易辛模型在反轉所有自旋之下是對稱的:一個外加的力場會破壞這種對稱。
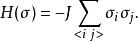 易辛模型
易辛模型 另一個常見的簡化是假設所有相鄰晶格點的互動作用都是相等的,因此可以設 J= J對於所有相鄰的 i, j∈Λ,而其哈密頓量可以寫:
特性
被研究的最透徹易辛模型是在 d維晶格上,平移不變、鐵磁性並且無外加場的模型。也就是 :Λ= Z, J=1, h=0。
易辛在他1924年的博士論文中,解決了在 d=1 時的情況 ,這個一維的模型可以想像成一排的自旋,而每個自旋都只和它左右兩邊的自旋互動作用。這個一模型不會產生相變,換句話說,對於所有正值的β,任意兩自旋的相關係數 都對 | i− j| 呈指數衰減:
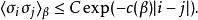 易辛模型
易辛模型 其中c(β)是一個只和β有關的函式。
由此可知。這個系統是無序的。根據一維模型的結論,易辛錯誤的認為任何維度的易辛模型都不會有相變。但事實上,在二維或二維以上的模型中,該系統可以歷經從無序相轉變成有序相的相變。基本上在β值小(高溫)時,系統處在無序相,而β值大(低溫)時,系統處在有序相中。換句話說,當系統在有序相時:
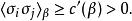 易辛模型
易辛模型 其中c'(β)也是一個只和β有關的函式。
這個性質是首先被魯道夫·佩爾斯(Rudolf Peierls)在1936年證明的,他的證法後來被稱為 佩爾斯論述(Peierls argument)。
在零磁下的二維方晶格易辛模型的解析解後來在1943年被昂薩格解出,他證明了該模型的相關函式和自由能可由一個無互動作用的格點費米子場(noninteracting lattice fermion)來界定。昂薩格在1949年發表了一個決定了自發磁化現象的公式,但卻沒有給出推導過程。後來是楊振寧在1951年發表了第一個正式的推導過程,其中裡面用到了包括塞格極限定理和弗雷德霍姆行列式等數學工具。
數值模擬
蒙特卡洛方法
易辛模型一般來說很難直接進行數值計算,因為他的自旋組態非常之多。考慮一個擁有 L個晶格點的模型,每個晶格點 σ有 ±1 兩種可能,因此所有的自旋組態共有 2種可能,這個數字會隨著 L的增加而進行指數增長。這也是為什麼一般在做易辛模型的數值模擬時,都會採用蒙特卡洛方法。
用蒙特卡洛方法來模擬易辛模型所用的哈密頓量為:
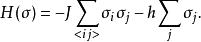 易辛模型
易辛模型 此外,可以假設外加磁場 ( h) 為零以簡化模型,因為大部分的問題都只需要用到零磁下的模型。因此,近一步簡化的哈密頓量為
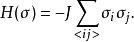 易辛模型
易辛模型 可以從這個模型計算出的物理量包括該系統在定溫下的比熱和磁化強度等等。
Metropolis 算法
Metropolis–Hastings算法是在數值模擬易辛模型時最常用的一種蒙特卡洛方法。這種方法首先要選定一個 選擇機率 g(μ, ν),代表系統在狀態μ下,在所有可能狀態中選到狀態ν的機率。另外還需定義出一個 接受機率 A(μ, ν) ,也就是說當系統在狀態μ下,接受系統跳到態ν的機率。如此的設計是為了讓系統達到細緻平衡。如果狀態ν被接受了,則整個系統就會跳到狀態ν,並且選擇和決定下一個要跳到的狀態。如果狀態ν被沒被接受,系統則留在狀態μ,一樣重新選擇下一個要跳到的狀態。這樣的步驟一直重複直到某些條件達成為止,譬如說整個易辛模型完全被磁化,也就是所有的自旋都只到同一個方向。另外在實行這種算法,有一點需要注意的是需要選到適當 g(μ, ν) 以保證整個過程的遍歷性(ergodicity)。
在熱平衡時,整個系統的能量只會有小幅度的擾動,這點促成了在演算時採用 單一自旋反轉法進行計算,也就是說每次系統轉換其狀態時,只改變其中一個自旋的方向。對自旋數很多的一易辛模型來說,系統在不同的狀態之間跳躍時,其能量改變的幅度都很小。事實上,對於每個晶格點都和 c個晶格點相鄰的模型來說,每次能量改變的最大幅度為 2 cJ。此外,採用這種單一自旋反轉法可以保證演算過程的遍歷性,因為任意一個狀態都可以藉由逐次的反轉相異的自旋,而變成任意其他狀態。
一維易辛模型
在一維易辛模型系統中,假設每個帶有自旋的原子分布在一維的圓圈中,且原子僅和鄰居發生互動作用,互動作用均為J,能量可表示為
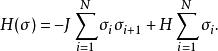 易辛模型
易辛模型 其中 h為外加磁場的強度, J為相鄰原子的耦合強度。該系統的自由能為:
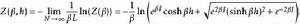 易辛模型
易辛模型 相鄰自旋的相關函式為:
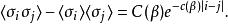 易辛模型
易辛模型 其中,C(β)和 c(β)是關於溫度的函式,當溫度 T> 0時取正值。當 T→ 0時, c(β)趨於零。
二維易辛模型
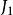 易辛模型
易辛模型 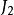 易辛模型
易辛模型 設二維方晶格易辛模型橫縱兩方向的互動作用能分別為和。拉斯·昂薩格求得無外磁矩,即 h=0時自由能的解析解:
 易辛模型
易辛模型 從自由能的偏導數可得到各種熱力學函式。
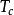 易辛模型
易辛模型 特別地,二維易辛模型有一個相變點,臨界溫度滿足以下方程:
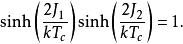 易辛模型
易辛模型 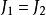 易辛模型
易辛模型 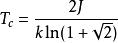 易辛模型
易辛模型 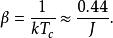 易辛模型
易辛模型 若,則,或

