背景
這一命題的逆命題:“等腰三角形兩底角的平分線長在相等”,早在二千多年前的《幾何原本》中就已作為定理,證明是很容易的。
1840年,德國數學家雷米歐斯給當時的大數學家斯圖姆的一封信中說到:“幾何題在沒有證明之前,很難說它是難還是容易。等腰三角形的兩底角平分線相等,國中生都會證明。但反過來,三角形的兩內角平分線相等,這個三角形一定是等腰三角形嗎?我至今還沒想出來。”
但上述命題在《幾何原本》中隻字未提,直到1840年,萊默斯(C.L.Lehmus)在他給斯圖姆(C.Sturm)的信中提出請求給出一個純幾何證明。斯圖姆沒有解決,就向許多數學家提出這一問題。首先給出證明的是瑞士幾何學家斯坦納(J.Steiner,1796~1863),因而這一定理就稱為斯坦納—萊默斯定理。
證明
德國數學家海塞(L.O.Hesse,1811~1874)的證法:
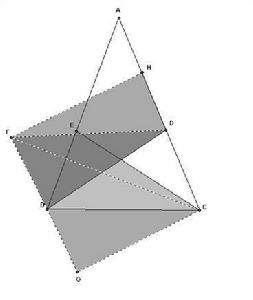
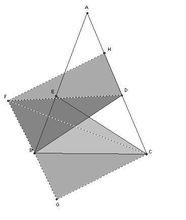 斯那坦問題
斯那坦問題作∠BDF=∠BCE;並使DF=BC
∵BD=EC,
∴△BDF≌△ECB,BF=BE,∠BEC=∠DBF.
設∠ABD=∠DBC=α,∠ACE=∠ECB=β,
∠FBC=∠BEC+α=180°-2α-β+α=180°-(α+β);
∠CDF=∠FDB+∠CDB=β+180-2β-α=180°-(α+β);
∴∠FBC=∠CDF,
∵2α+2β<180°,
∴α+β<90°,
∴∠FBC=∠CDF>90°
∴過C點作FB的垂線和過F點作CD的垂線必都在FB和CD的延長線上.
設垂足分別為G、H;∠HDF=∠CBG;∵BC=DF,∴Rt△CGB≌Rt△FHD,∴CG=FH,BC=HD
連線CF,∵CF=FC,FH=CG,∴Rt△CGF≌△FHC(HL),∴FG=CH, 又∵BG=DH,∴BF=CD, 又∵BF=BE,∴CD=BE,∵BE=CD,BC=CB,EC=DB,∴△BEC≌△CDB,∴∠ABC=∠ACB
∴AB=AC.
其他證明
證明一
設三角形ABC,角B、角C的平分線是BE、CD
作∠BEF=∠BCD;並使EF=BC
∵BE=DC
∴△BEF≌△DCB,BF=BD,∠BDC=∠EBF
設∠ABE=∠EBC=α,∠ACD=∠DCB=β
∠FBC=∠BDC+α=180°-2α-β+α=180°-(α+β);
∠CEF=∠FEB+∠CEB=β+180-2β-α=180°-(α+β);
∴∠FBC=∠CEF
∵2α+2β<180°,∴α+β<90°
∴∠FBC=∠CEF>90°
∴過C點作FB的垂線和過F點作CE的垂線必都在FB和CE的延長線上.
設垂足分別為G、H;
∠HEF=∠CBG;
∵BC=EF,
∴Rt△CGB≌Rt△FHE
∴CG=FH,BG=HE
連線CF
∵CF=FC,FH=CG
∴Rt△CGF≌△FHC
∴FG=CH,∴BF=CE,∴CE=BD
∵BD=CE,BC=CB,∴△BDC≌△CEB
∴∠ABC=∠ACB
∴AB=AC
證明二
設二角的一半分別為α、β
sin(2α+β)/ sin2α= BC/CE = BC/BD = sin(α+2β)/ sin2β,
∴2sinαcosαsin(α+2β) - 2sinβcosβsin(2α+β) =0
→sinα[sin2(α+β)+sin 2β]- sinβ[sin2(α+β)+ sin2α]=0
→sin2(α+β)[sinα-sinβ]+2 sinαsinβ[cosβ- cosα]=0
→sin [(α-β)/2][sin2(α+β) cos[(α+β)/2] + 2 sinαsinβsin [(α+β)/2]=0
,∴sin[(α-β)/2]=0
∴α=β,∴AB=AC.
證明三
用張角定理:
2cosα/BE=1/BC+1/AB
2cosβ/CD=1/BC+1/AC
若α>β 可推出AB>AC矛盾!
若α<β 可推出AB
所以AB=AC
後世發展
斯坦納的證明發表後,引起了數學界極大反響。論證這個定理的文章發表在1842年到1864年的幾乎每一年的各種雜誌上。後來,一家數學刊物公開徵解,竟然收集並整理了60多種證法,編成一本書。直到1980年,美國《數學老師》月刊還登載了這個定理的研究現狀,隨後又收到了2000多封來信,增補了20多種證法並收到了一個最簡單的直接證法。經過幾代人的努力,100多年的研究,“斯坦納-雷米歐斯”定理已成為數學百花園中最惹人喜愛的瑰麗花朵!