簡介
數據流分析是一項編譯時使用的技術,它能從程式代碼中收集程式的語義信息,並通過代數的方法在編譯時確定變數的定義和使用。通過數據流分析,可以不必實際運行程式就能夠發現程式運行時的行為,這樣可以幫助大家理解程式。數據流分析被用於解決編譯最佳化、程式驗證、調試、測試、並行、向量化和片行編程環境等問題。
數據流的介紹
控制流圖
理解數據流分析的一個預備概念是控制流圖(control flow graph,簡稱CFG),簡而言之就是流圖。CFG是一個有向圖,它包含一部分程式的控制流。CFG典型的套用是代表類似過程大小的程式片斷。
典型的流圖結點是基本塊(總是順序執行的代碼片斷),流圖的邊代表基本塊之間可能存在的控制流,其中的一個結點被標明為開始。
路徑謂詞
控制流分析跟蹤程式可能執行的路徑,數據流分析沿著可能的控制流路徑跟蹤數據可能的定義和使用,並收集有關特定數據項屬性的信息。從根本上來說,數據流分析的目的是確定路徑謂詞的真或假。路徑謂詞是一些語句,這些語句表示在程式執行當中沿著一定的控制流路徑發生了什麼,在所有這些路徑上使用任意或存在量詞對語句進行量化。路徑的定義與CFG有關,一條控制流路經是在CFG中的一條路徑。
標準數據流問題
數據流分析包括過程內的和過程間的數據流分析。常見的過程內數據流問題包括:到達定值,活躍使用,可用表達式和頻繁使用,可用表達式和頻繁使用。過程間數據流問題包括:形式邊界集合,可能別名和可能被修改。另外,過程內的數據流問題在過程間數據流分析中也會出現。
數據流分析算法
目前出現的許多數據流算法可以被歸類為:疊代算法,消除算法,及可達性算法。
疊代算法
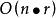 數據流分析
數據流分析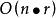 數據流分析
數據流分析 數據流分析
數據流分析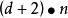 數據流分析
數據流分析選代算法通過初始化節點變數為一些可靠的值,並且連續地計算這些變數值,直到到達一個固定點,來解決等式系統。對於round robin版本的疊代算法是重複計算所有節點的數據流屬性,直到屬性值穩定。如果位向量的大小是r,計算複雜度為。這樣,最壞情況下在圖上可能有次疊代,每次疊代涉及n個節點屬性的計算。如果所有的r位能夠一步被處理,複雜性就變成。在單向問題中數據流只朝著一個方向,節點被後序遍歷還是逆後序遍歷依數據流的方向而定。這樣d+2次疊代就足夠了,這裡d是流圖深度的6次方,因此複雜性是。
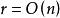 數據流分析
數據流分析 數據流分析
數據流分析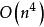 數據流分析
數據流分析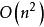 數據流分析
數據流分析對於的程式,所有的r位向量不能被一步處理,而處理一個r位的位向量本身將需要步,因此疊代方法的複雜度的上下界分別為和。
消除算法
消除算法通過利用流圖的結構屬性減少解決數據沉問題所需要的大量工作。通過連續的套用圖的轉換使流圖歸約到一個點,圖的轉換就是使用圖的分析或圖的分裂去分析區間以獲得一個派生圖。在一個區間內,數據流的屬性是由區間內頭節點的數據流的屬性來確定的。這樣可以延遲替代聯立方程中的些值。對於單向流問題,這些方法典型的複雜度為O(N),這裡N是在歸約圖序列中節點的總數。儘管它們已經被用於解決一類受限制的雙向問題,但消除算法不能被擴展到一般的雙向數據流問題。
可達性算法
可達性算法是由哥本哈根大學的Thomas Reps及Mooly Sagiv等人在1994年提出來的。可達性算法把過程問數據流問題轉換成一種特殊的圖形可達性問題(可達性是指沿著過程問間可實現路徑),然後解決通過有效的圖的算法。該算法的局限在於數據流實際匕是一個有限的集合,並且數據流函式分布在集合操作(並或交)上。
該算法解決了一大類過程間的數據流分析問題,從時間複雜度來看,它是多項式時間算法。
分析方法
數據流信息的計算非常複雜,尤其是過程問數據流分析,由於過程間的調用關係比較複雜,使得靜態的數據流分析更為困難。然而在所有程式點計算完整的數據流信息並不總是必要的,所以文章提出了需求過程間數據流分析方法。該分析方法在很多方面比完全分析是更可取的。
它能縮小感興趣點的焦點:所使用的數據流分析軟體工具經常需要的信息僅在某些特定的程式點的集合。在程式的最佳化階段,儘管轉換可以被組織在一些熱點,但在早期階段需要使用完全數據流分析確定數據流事實。需求算法可以大量地減少需要計算的外部信息。
它能縮小感興趣的專門的數據流事實的焦點:儘管在每個程式點P數據流信息是需要的,但在P點的整個數據流的集合是不需要的。
減少初步階段的工作:在那些能被分成獨立階段的問題中,並非上一階段所有的信息對下一階段束說都是必要的。需求算法可以減少花費在準備階段或其他輔助階段的大量工作。
需求分析作為一個用戶級的操作:人們希望有一個程式開發工具,用戶能夠向它互動地提問關於程式各個方面的問題。當要理解複雜的代碼時這種工具是非常有用的。
需求過程間數據流分析方法的主要思想是:僅為感興趣的單個程式元素(或少數感興趣的元素)報告扼要信息(summalyinformation)。因為在一個程式點的扼要信息決定於在其他點的扼要信息,在這些點上需要計算其扼要信息(或者計算其信息的數量),所以最重要的就是最小化其他點的數目。
從該思想出發,把獲得需求算法分為兩個階段:
(1) 把過程間數據流的完全算法編碼成一個邏輯程式;
(2) 通過套用一個轉換-稱為Alexander方法或魔術集合轉換,把完全算法轉換為一個需求算法。
以Sharir和Pnueli的過程間的“函式方法”為基礎進行了驗證,結果證明該方法是實際可行的。
展望
數據流分析技術對於分析程式行為來說是一項有力的技術。然而,大量的工作都是相對於順序化的程式做的,對並發程式的數據流分析的工作很少。因此,數據流技術今後的發展除了要研究出更有效、更準確、更快速的算法外,還要開發出引對並發程式的數據流分析技術。