背景
在數位訊號接收中，濾波器的作用有兩個方面：
第一是使濾波器輸出有用信號成分儘可能強；
第二是抑制信號帶外噪聲，使濾波器輸出噪聲成分儘可能小，減小噪聲對信號判決的影響。
通常對最佳線性濾波器的設計有兩種準則：
一種是使濾波器輸出的信號波形與傳送信號波形之間的均方誤差最小，由此而導出的最佳線性濾波器稱為維納濾波器；
另一種是使濾波器輸出信噪比在某一特定時刻達到最大，由此而導出的最佳線性濾波器稱為匹配濾波器。
在數字通信後者，匹配濾波器具有更廣泛的套用。
基本原理
1.匹配濾波器的原理
匹配濾波的基本原理為：在輸入為確知信號加白噪聲的情況下，所得輸出信噪比最大的線性濾波器就是匹配濾波器。
匹配濾波器是數字通信系統（包括數字基帶傳輸系統和數字調製傳輸系統）中的重要部件，它在數位訊號和雷達信號的檢測中具有特別重要的意義。
由數位訊號的判決原理可知，抽樣判決器輸出數據正確與否，與濾波器輸出信號波形和傳送信號波形之間的相似程度無關，也即與濾波器輸出信號波形的失真程度無關，而只取決於抽樣時刻信號的瞬時功率與噪聲平均功率之比，即信噪比。信噪比越大，錯誤判決的機率就越小；反之，信噪比越小，錯誤判決的機率就越大。[2]
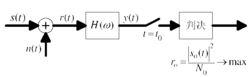圖1 數位訊號接收等效原理圖匹配濾波器是一個最佳線性濾波器，在輸入為已知信號加白噪聲的情況下，能使輸出的信噪比最大，從而實現對信號的最佳接收。也就是說，當我們能最佳地判斷信號的出現時，系統的檢測性能就可以提高，而只有使得濾波器獲得最大的信噪比，才能最佳地判斷信號的出現。
2.匹配濾波器的傳輸函式
所謂的最優濾波器，實際上都是在某個準則下的最優。匹配濾波器對應的最優的準則是輸出信噪比（SNR）最大。而且還有一個前提條件是在白噪聲背景下。
設輸入端的輸入信號和噪聲的混合波形為：
X(t)=s(t)+n(t)
其中，s(t)為輸入信號，其頻譜函式為S(ω),n(t)為功率譜密度是n0/2的高斯白噪聲，H(ω)是匹配濾波器的傳輸函式。
根據線性電路的疊加原理，濾波器的輸出也包含有信號和噪聲兩個部分，即：
Y(t)=s0(t)=n0(t)
輸入信號s(t)通過濾波器後的回響s0(t)可以表示為：
S0(t)=1/(2*π)*∫H(ω)S(ω)edω
積分區間為從負無窮到正無窮之間。
匹配濾波器在t=t0時刻輸出的抽樣值為：
S0(t0)=1/(2*π)*∫H(ω)S(ω)edω
在抽樣時刻，匹配濾波器輸出信號的瞬時功率為：
S0=|s0(t0)|=|1/(2*π)*∫H(ω)S(ω)edω|
輸出噪聲平均功率為：
N0=1/(2π)* ∫|H(ω)|*(n0/2)*dω= n0/(4π)* ∫|H(ω)| dω
則匹配濾波器在t0時刻的輸出信噪比r0為：
r0=S0/N0=|1/(2*π)*∫H(ω)S(ω)edω|/{ n0/(4π)* ∫|H(ω)| dω} （1）
表示的是輸出信號瞬時功率與輸出噪聲平均功率之比。
由上式（1）可知，濾波器的輸出信噪比r0與輸入信號的頻譜函式S(ω)和濾波器的傳輸函式H(ω)有關，當輸入信號給定時，r0隻與濾波器的傳輸函式H(ω)有關。
對上式求極值可以得到該濾波器所能給出的最大輸出信噪比為：
r=2E/n0
其中，E為信號s(t)的總能量：
E=(1/2π)* ∫|S(ω)| dω
要使匹配濾波器的輸出信噪比最大，則傳輸函式為：
H(ω)=KS(ω)e
K為任意常數，S(ω)為S(ω)的復共軛。
在白噪聲干擾的背景下，匹配濾波器在給定時刻上獲得最大的輸出信噪比。這種濾波器就是最大信噪比意義下的最佳線性濾波器，即匹配濾波器。
匹配濾波器的單位衝激回響可以表示為：
h(t)=Ks(t0-t)
也就是說，匹配濾波器的輸入信號波形s(t)在時間軸上的鏡像波形s(-t)平移得到的波形就是匹配濾波器的衝激回響h(t)。對於一個物理可實現的匹配濾波器，在輸出最大的信噪比時刻t0之前，輸入信號s(t)必須消失。即其輸出最大信噪比時刻t0必須在輸入信號結束之後。
當輸入信號為s(t)時，則匹配濾波器的輸出信號為：
s0=s(t)*h(t)= ∫s(t-τ)h(τ)dτ
=∫s(t-τ)Ks(t0-τ)dτ
令t0=τ-x，則：
s0(t)=K∫s()s(x+τ-t0)dx=KR(t-t0)
在上式中，R(t)為輸入信號的自相關函式。由上式可以看出，匹配濾波器的輸出信號的是輸入信號自相關函式的K倍，所以匹配濾波器可以看成是一個相關器。並在t0時刻達到最大輸出信噪比。由於常數K與輸出信噪比無關，通常取K=1。
3.匹配濾波器的物理解釋
從匹配濾波器的傳輸函式以及單位衝激回響表達式可以看出，匹配濾波器的頻率回響使輸入信號頻率回響的共軛。從物理上直觀解釋匹配濾波器為：
一方面，從幅頻特性來看，匹配濾波器和輸入信號的幅頻特性完全一樣。也就是說，在信號越強的頻率點，濾波器的放大倍數也越大；在信號越弱的頻率點，濾波器的放大倍數也越小。這就是信號處理中的“馬太效應”。也就是說，匹配濾波器是讓信號儘可能通過，而不管噪聲的特性。因為匹配濾波器的一個前提是白噪聲，也即噪聲的功率譜是平坦的，在各個頻率點都一樣。因此，這種情況下，讓信號儘可能通過，實際上也隱含著儘量減少噪聲的通過。這正是使得輸出的信噪比最大。
另外一方面，從相頻特性上看，匹配濾波器的相頻特性和輸入信號的相頻特性完全相反。這樣，通過匹配濾波器後，信號的相位為0，正好能實現信號時域上的相干疊加。而噪聲的相位是隨機的，只能實現非相干疊加。這樣在時域上保證了輸出信噪比的最大。
實際上，在信號與系統的幅頻特性與相頻特性中，幅頻特性更多地表征了頻率特性，而相頻特性更多地表征了時間特性。匹配濾波器無論是從時域還是從頻域，都充分保證了信號盡肯能大地通過，噪聲儘可能小地通過，因此能獲得最大信噪比的輸出。
實際上，匹配濾波器由其命名即可知道其鮮明的特點，即濾波器是匹配輸入信號的。一旦輸入信號發生了變化，原來的匹配濾波器就再不能成為匹配濾波器了。由此，很容易聯想到相關這個概念，相關的物理意義就是比較兩個信號的相似程度。如果兩個信號完全一樣，就是匹配。事實上，匹配濾波器的另外一個名字就是相關接收，兩者表征的意義是完全一樣的。只是匹配濾波器著重在頻域的表征，而相關接收則著重在時域的表述。
因此，理解匹配濾波器的概念應注意三個問題：
（a）白噪聲背景是推導匹配濾波器的前提，但在實際套用中，白噪聲背景不是套用匹配濾波器的前提。實際Ixtapa的噪聲都不完全是白噪聲，但也能使用匹配濾波器，因為實際系統的噪聲中白噪聲所占比例很大，一般達到90%以上，可以近似當做白噪聲來處理。匹配濾波器套用的前提條件是輸入信號的形式已知；
（b）匹配濾波器關心的是如何在含有噪聲的信號中發現目標回波，而不關心信號波形是否失真。因此，匹配濾波器不能用於波形估計的場合，波形估計要用維納濾波或Kalman濾波等一類方法；
（c）匹配濾波器是一種線性濾波器，它的輸出信噪比不是在所有類型（包括線性和非線性）濾波器中最大的，而是線上性濾波器中能夠得到最大的輸出信噪比。某些情況下，非線性濾波能夠得到比匹配濾波器更大的輸出信噪比。
4.匹配濾波器的作用
（1）濾波器的相頻特性與信號相頻特性共軛，使得輸出信號所有頻率分量都在輸出端同相疊加而形成峰值。
（2）按照信號的幅頻特性對輸入波形進行加權，以便最有效地接收信號能量而抑制干擾的輸出功率。即當信號與噪聲同時進入濾波器時，它使信號成分在某一瞬間出現尖峰值，而噪聲成分受到抑制。
5.匹配濾波器的設計
採用高效的數字匹配濾波器設計時數字接收機中提高信噪比改善系統信號處理性能的一項關鍵技術。
幾種常用的匹配濾波器。
直接形式的匹配濾波器、轉置結構的匹配濾波器、採用分散式算法的匹配濾波器和摺疊式匹配濾波器。
（1）直接形式的匹配濾波器
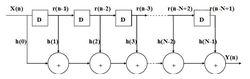圖2直接形式的匹配濾波器結構框圖圖2所示為直接形式的匹配濾波器，這種結構主要由移位暫存器、加法器、乘法器組成。這種結構在實際使用中可以按照流水線的設計思想，使得加法器分級運算，可以提高處理速度。不過，這種結構由於大量的加法器和乘法器，消耗了大量的LC(logic element)資源。
（2）轉置結構的FIR濾波器
圖3所示是轉置結構的FIR濾波器，這種結構的好處是不需要輸入信號x(n)提供額外的移位暫存器，而且沒必要為達到高吞吐量而為乘法器添加額外的流水線級。
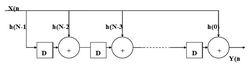圖3轉置結構的FIR濾波器（3）採用分散式算法的FIR濾波器
分散式算法時一項重要的FPGA技術，廣泛套用於乘積和之中。算法實現中需要藉助一個LUT來完成。分散式算法的好處是對於階數不高的濾波器占用資源少。缺點是隨著級數的增加，LUT會變得很龐大，甚至不可實現。另外，由於每進入一位數據要進行N次查詢和累加運算才能得到最後的結果，所以對時鐘速度要求很高。
（4）摺疊式濾波器
圖4所示為摺疊式FIR濾波器結構，這種結構是在轉置結構濾波器的基礎上發展起來的，與轉置結構濾波器不同的地方在於：FIR濾波器是依靠提高系統工作時鐘來完成乘法器和加法器的復用，相對其他結構最合適實現匹配濾波器。其資源消耗主要和下面因素有關：偽碼長度、過採樣率、信號量化的位寬、摺疊的次數。
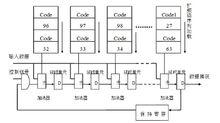圖4摺疊式濾波器結構示意圖整個系統的工作速度主要取決於加法器和移位暫存器的工作速度。對於碼長很大的序列，可以適當增加摺疊次數，以提高系統的工作時鐘來減少資源消耗。
匹配濾波器的套用
匹配濾波器廣泛用於雷達、聲納和通信。
對於大事件頻寬積信號，匹配濾波器等效於脈衝壓縮。因此可以提高雷達或聲納的距離解析度和距離測量精度。在擴頻通信中，可以實現解擴。
實際系統中的匹配濾波器的確都存在一定程度的失配。比如在雷達系統中，由於目標反射的調製作用，目標的回波不僅在包絡上會出現調製（低頻調製），而且由於目標運動會帶來都卜勒調製，使回波信號附加一個都卜勒頻移。匹配濾波器一定程度的失配使濾波性能損失一點，但這並不妨礙匹配濾波器的使用。在通信系統中引起匹配濾波器失配的主要原因就是信道衰減，這種衰減可能對不同頻率成分的信號衰減程度不一樣，就像雷達目標回波中的包絡一樣會出現低頻調製，但這種調製帶來的影響比目標回波的都卜勒頻移要小得多。因此，理論上通信系統中的匹配濾波效果比雷達系統的更好。
