散列樹

HashNode();//默認構造函式 HashNode(T1 ~HashNode();

散列樹

我們選擇質數分辨算法來建立一棵散列樹（Hash樹）。
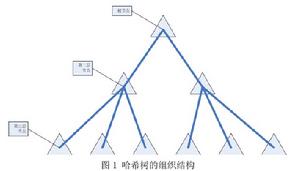
選擇從2開始的連續質數來建立一個十層的哈希樹。第一層結點為根結點，根結點下有2個結點；第二層的每個結點下有3個結點；依此類推，即每層結點的子節點數目為連續的質數。到第十層，每個結點下有29個結點。如下圖所示：

同一結點中的子結點，從左到右代表不同的餘數結果。
例如：第二層結點下有三個子節點。那么從左到右分別代表：除3餘0，除3餘1，除3餘2.
對質數進行取余操作得到的餘數決定了處理的路徑。結點：結點的關鍵字(在整個樹中是唯一的)，結點的數據對象，結點是否被占據的標誌位(標誌位為真時，關鍵字才被認為是有效的)，和結點的子結點數組。

特點

1.哈希樹的結構是動態的，也不像某些哈希算法那樣需要長時間的初始化過程，只需要初始化根結點就可以開始工作。哈希樹也沒 有必要為不存在的關鍵字提前分配空間。2.查找迅速，最多只需要10次取余和比較操作，就可知道這個對象是否存在。哈希樹的查找次數和元素個數沒有關係。3.結構不變，哈希樹在刪除的時候並不做任何結構調整。這也是它的一個非常好的優點。常規樹結構在增加元素和刪除元素的時候都要做一定的結構調整。4.非排序性，哈希樹不支持排序，沒有順序特性。需要注意的是：哈希樹是一個單向增加的結構，即隨著所需要存儲的數據量增加而增大。即使數據量減少到原來的數量，但是哈希樹的總結點樹不會減少。這樣做的目的是為了避免結構的調整帶來的額外消耗。

C代碼

// HashTree.cpp : 定義控制台應用程式的入口點。

//選擇質數分辨算法構造一棵哈希樹

#include "stdafx.h"

#include <iostream>

using namespace std;

const int SIZE = 32;//第10個質數為29，餘數不可能大於32，所以數組的固定長度設定為32

const int Prime[10] = {2,3,5,7,11,13,17,19,23,29};

//哈希結點類型

template<class T1, class T2>

class HashNode

{

public:

HashNode();//默認構造函式

HashNode(T1 key, T2 value);//一般構造函式

~HashNode();

public:

T1 m_key; //結點的關鍵字

T2 m_value; //結點的數據對象

bool occupied; //結點是否被占據，如果是表示結點的關鍵字有效

HashNode *child[SIZE]; //結點的子結點數組

};

template<class T1, class T2>

HashNode<T1,T2>::HashNode()

{

occupied=false;

memset(child, NULL, SIZE*sizeof(HashNode<T1,T2>*));

}

template<class T1, class T2>

HashNode<T1,T2>::HashNode(T1 key, T2 value)

{

this->m_key = key;

this->m_value = value;

occupied=false;

memset(child, NULL, SIZE*sizeof(HashNode<T1,T2>*));

}

template<class T1, class T2>

HashNode<T1,T2>::~HashNode()

{

}

//哈希樹類型

template<class T1, class T2>

class HashTree

{

public:

HashTree();

~HashTree();

void InsertNode(T1 key, T2 value);

bool FindNode(T1 key, T2 &value);

void DeleteNode(T1 key);

private:

HashNode<T1,T2> *root;

void Insert(HashNode<T1,T2> *hashNode, int level, T1 key, T2 value);//插入結點

bool Find(HashNode<T1,T2> *hashNode, int level, T1 key, T2 value);//查找

void Delete(HashNode<T1,T2> *hashNode, int level,T1 key);//刪除結點

};

template<class T1, class T2>

HashTree<T1,T2>::HashTree()

{

root = new HashNode<T1,T2>;

}

template<class T1, class T2>

HashTree<T1,T2>::~HashTree()

{

}

template<class T1, class T2>

void HashTree<T1,T2>::InsertNode(T1 key, T2 value)

{

Insert(root,0,key,value);

}

template<class T1, class T2>

void HashTree<T1,T2>::Insert(HashNode<T1, T2> *hashNode, int level, T1 key, T2 value)//插入結點

{

if(hashNode->occupied == false)

{

hashNode->m_key = key;

hashNode->m_value = value;

hashNode->occupied = true;

return;

}

int index = key%Prime[level];

if (hashNode->child[index] == NULL)

{

hashNode->child[index] = new HashNode<T1,T2>;

}

level += 1;

Insert(hashNode->child[index], level, key, value);

}

template<class T1, class T2>

bool HashTree<T1,T2>::FindNode(T1 key, T2 &value)

{

return Find(root, 0, key, value);

}

template<class T1, class T2>

bool HashTree<T1,T2>::Find(HashNode<T1,T2> *hashNode, int level, T1 key, T2 value)//查找

{

if (hashNode->occupied == true)

{

if (hashNode->m_key == key)

{

value = hashNode->m_value;

return true;

}

}

int index = key%Prime[level];

if (hashNode->child[index] == NULL)

{

return false;

}

level += 1;

return Find(hashNode->child[index], level, key, value);

}

template<class T1, class T2>

void HashTree<T1,T2>::DeleteNode(T1 key)

{

Delete(root, 0, key);

}

template<class T1, class T2>

void HashTree<T1,T2>::Delete(HashNode<T1,T2> *hashNode, int level, T1 key)//刪除結點

{

if (hashNode->occupied == true)

{

if (hashNode->m_key == key)

{

hashNode->occupied = false;

cout << "關鍵字為" << key << "結點已被刪除！" << endl;

return;

}

}

int index = key%Prime[level];

if (hashNode->child[index] == NULL)

{

cout << "該關鍵字不存在！" << endl;

return;

}

level += 1;

Delete(hashNode->child[index], level, key);

}

int _tmain(int argc, _TCHAR* argv[])

{

HashTree<int, int> ht;

ht.InsertNode(1, 8);

ht.InsertNode(2, 0);

ht.InsertNode(3, 4);

ht.InsertNode(4, 7);

ht.InsertNode(5, 4);

ht.InsertNode(6, 3);

ht.InsertNode(7, 8);

int nvalue = 0;

cout << ht.FindNode(5,nvalue) << endl;

cout << ht.FindNode(9,nvalue) << endl;

ht.DeleteNode(4);

ht.DeleteNode(10);

cout<<"baasdfas"<<endl;

system("pause");

return 0;

}