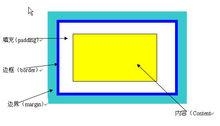
邊界值
定義
邊界是指相對於輸入等價類和輸出等價類而言,稍高於其邊界值及稍低於其邊界值的一些特定情況。基於邊界的方法是根據定義域來實現的,最終演變成邊界值分析、健壯性測試、最壞情況測試和健壯最壞情況測試四種技術。
邊界值分析也是一種黑盒測試方法,是對等價類分析方法的一種補充,由長期的測試工作經驗得知,大量的錯誤是發生在輸入或輸出的邊界上。因此針對各種邊界情況設計測試用例,可以查出更多的錯誤。
關注
邊界值分析關注的是輸入空間邊界,用以標識測試用例,基本思想是在最小值(min)、略高於最小值(min+)、正常值(nom)、略低於最大值(max-)和最大值(max)等處取值。邊界值分析手段主要有兩種方式:通過變數數量和通過值域的種類進行。如一個n變數函式f(x1,x2,……xn)按以上方式每次確定一個測試對象(基於“單缺陷假設”理論),會產生4n+1個測試用例。健壯性測試是擴展邊界值分析的測試,即增加一個略大於最大值(max+)和略小於最小值(min-)的取值,則用例數將變為6n+1。當邊界值變數不是獨立變數時,則以上測試用例就顯的不充分。對於邏輯變數而言這種用例也沒有什麼用處。
最壞情況測試
拒絕“單缺陷假設”理論的情況下,對所有變數的邊界值集合進行5元素笛卡兒積計算,用以生成測試用例,對於n變數函式的最壞測試基於邊界值分析會產生5n個測試用例,基於健壯性分析則產生7n個測試用例。相比而言最壞情況測試代價較高,因此其最佳運用是物理變數具有大量互動作用,或者函式失效的代價極高的情況下。
①“在最小值、和最大值處”是指的一般邊界值分析。
②“略小於最小值、最小值、略高於最小值、正常值、略低於最大值、最大值、略大於最大值”其實是健壯性邊界值分析,也就是考慮了非法的意外值。
③可靠性理論“單缺陷假設”:失效極少是由兩個(或多個)缺陷的同時發生引起的。
 擴展邊界法
擴展邊界法原則
一、如果輸入條件規定了值的範圍,則應該取剛達到這個範圍的邊界值,以及剛剛超過這個範圍邊界的值作為測試輸入數據;
二、如果輸入條件規定了值的個數,則用最大個數、最小個數、比最大個數多1格、比最小個數少1個的數做為測試數據;
三、根據規格說明的每一個輸出條件,使用規則一;
四、根據規格說明的每一個輸出條件,使用規則二;
五、如果程式的規格說明給出的輸入域或輸出域是有序集合(如有序表、順序檔案等),則應選取集合的第一個和最後一個元素作為測試用例;
六、如果程式用了一個內部結構,應該選取這個內部數據結構的邊界值作為測試用例;
七、分析規格說明,找出其他可能的邊界條件。
 邊界值法
邊界值法擴展邊界條件法
擴展邊界條件法簡稱EBC法。最早是由P.C.Waterman提出來的,原用來求解導體的散射問題,後來推廣套用到求解介質體,它的求解
步驟如下:
(1)採用等效原理,由外等效法以介質表面S上的電磁流替換介質體,此表面電磁流在S面外產生散射場,而在S面內產生與人射場大小相等方向相反的電磁場一Er與一r使S面的內場為零’。
(2)將採用等效原理得到的積分方程中的人射場和介質體內的場量均展開為矢量球面波函式。
(3)在S面上引用切向場連續的邊界條件就可解得用人射場的展升係數表達的內場展開式中的待定係數。
(4)求出S面上內場的切向分量,由此解出散射場。
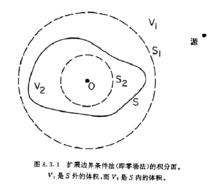
Waterman(1969,,1971)建立的擴展邊界條件(EBC)法又稱為零場法,它是求解面積分方程的方法之一。在該方法裡,積分方程不直接加於表面S上,而是加於如圖所示的S之外的表面S1和S2上以簡化方程的求解。
 擴展邊界法
擴展邊界法標量場情況
標量積分方程為
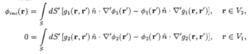 擴展邊界法
擴展邊界法其中方程(1)適用於S包圍的V內的任何地方,而方程(2)適用於S外的V任意地方。如果將積分方程(1)套用於V內的一個球面S上,將積分方程(2)套用於V內的一個球面S,則通常比較方便。這樣做的另一優點是積分方程的解得到了簡化。在這一方法裡,積分方程施加於物體表面之外的一些表面上,故得名為擴展邊界條件法(簡稱EBC法)。
如果用球諧函式展開場量,則在球面上的積分方程可以得到簡化。例如,由加法定理,均勻介質的格林函式可展開。
但在實際套用中,通過捨去無限維數矩陣方程的高階項,可以解出真與入射場幅度的關係。
在擴展邊界條件法中,場僅僅在S以內和S1以外被抵消。事實上,加在S1的表面源也會抵消S以內任何一點或S以外任何一點的某些場。這樣,擴展邊界條件法所提供的解有時是實際解的近似,儘管在很多情形中,這種近似是非常好的。
由於檢驗表面S和S在擴展邊界條件中總是處於表面S之外,所以如果S和S離開S的最大距離很大的話。矩陣方程將變得非常病態。例如,對於細長物體或呈波紋狀的物體,便會出現上述問題。從物理上講,對於這樣的表面,在S上的表面源產生的場局部地集中於S的附近,使得問題變得病態(在平面波紋面的情況下,這種局部場其實是雕落波)。相應地,這些場在S上的信息在5:和S。上受到了大大削減,所以將積分方程施加於S和S上便得到了病態的方程。
Waterman的EBC法的收斂問題已由Bolomey和Wirgin(1974)及Bates和Wall(1977)研究過。儘管如此,由:屍它產生的方程較為簡單,EBC法在很多套用問題里都是很有吸引力的。對於散射體周圍的場可展開為球諧函式、柱諧函式,或伏洛蓋(Floguet)模(如周期性粗糙表面)的情形,EBC法特別方便。
EBC法也很容易套用於不可貫穿物體。在此情況下,我們只需求解方程,其邊界條件為齊次荻里赫萊或紐曼邊界條件,或者是阻抗邊界條件。由於完全不同的原因,由此推導的矩陣是病態的。這一內共振問題可以通過選擇一個完備集來展開表面源而得到解決(見Waterman 1969)。
