數學模型
在控制系統的分析設計中,首先要建立控制系統的數學模型,數學模型是描述系統內部物理量(或變數)之間的關係的數學表達式。建立控制系統數學模型的方法通常有分析法和實驗法兩種。
(1)分析法
需要已知系統各部分依據的物理規律或化學規律列出相應方程。
(2)實驗法
實驗法人為地給系統施加某種測試信號,記錄其輸出回響,並用適當的數學模型去逼近,這種方式又稱為系統辨識。
在使用分析法進行系統建模時,常見的模型有時域模型、復域模型。
時域模型
使用微分方程描述的系統模型稱為時域模型。在給定外作用及初始條件下,求解微分方程可以獲得系統的輸出回響。這種方法比較直觀,有助於藉助計算機迅速求得結果。但如果系統結構改變或某幾個參數改變時,就要重新列方程求解,不便於系統分析和設計。
復域模型
使用拉氏變換法求解線性系統的微分方程時,可以得到控制系統在複數域的數學模型:傳遞函式。傳遞函式不僅可以表征系統的動態性能,而且可以用來研究系統結構或參數變化對系統性能的影響。
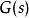 控制性能
控制性能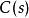 控制性能
控制性能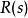 控制性能
控制性能傳遞函式定義:線性定常系統的傳遞函式 ,定義為零初始條件下,系統輸出量的拉氏變換 ,與輸入量的拉氏變換 之比。
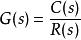 控制性能
控制性能傳遞函式的性質
(1)傳遞函式是復變數s的有理真分式函式,具有複變函數的所有性質。
(2)傳遞函式是一種用系統參數表示輸入量與輸出量之間關係的表達式,只取決於系統或元件的結構和參數,而與輸入量的形式無關。
(3)傳遞函式與微分方程有相通性,兩者(兩個類型的系統模型)可以用d/dt與s互相置換的方式變換。
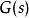 控制性能
控制性能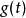 控制性能
控制性能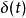 控制性能
控制性能(4) 的拉氏反變換是脈衝回響 ,即脈衝函式 輸入時的輸出回響。
性能指標
控制系統性能評價分為動態性能指標和穩態性能指標兩類。為了求解系統的時間回響(我們關注的性質)。必須了解輸入信號(即外作用)的解析表達式。然而在一般情況下,外加輸入有隨機性無法預知。
典型輸入信號
研究分析系統的性能指標時,通常選擇若干典型輸入信號作為動態性能指標和穩態性能測試之用,典型輸入信號包括:
•單位階躍函式
•單位斜坡函式
•單位加速度函式
•單位脈衝函式
•正弦函式
實際中採用上述哪種典型輸入信號取決於系統常見的工作狀態。同時,在所有可能的輸入信號中,選擇最不利的信號作為典型輸入信號測試系統指標。在典型輸入信號作用下,任何控制系統的時間回響都有動態過程和穩態過程兩部分組成。因此,系統的時間回響、動態、穩態過程與動態、穩態性能指標以及典型輸入信號的關係如圖1所示。
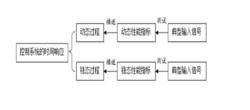 圖1
圖1動態指標
(1)動態過程
動態過程又稱過渡過程或瞬態過程,指系統在典型輸入信號作用下,系統輸出量從初始狀態到最終狀態的回響過程。由於實際控制系統具有慣性、摩擦及其他原因,系統輸出量不可能完全復現輸入量的變化。根據系統結構和參數的選擇,動態過程表現為衰減、發散、等幅振盪等形式。
(2)動態性能
系統的動態過程提供系統穩定性、回響速度及阻尼情況,由動態性能指標描述。通常在階躍函式作用下,測定或計算系統的動態性能。描述穩定的系統在單位階躍函式的作用下,動態過程隨時間t的變化狀況的指標,稱為動態性能指標。系統的單位階躍回響如圖2所示。
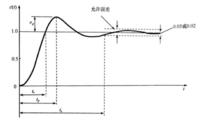 圖2 系統的單位階躍響
圖2 系統的單位階躍響上升時間(rise time)t
 控制性能
控制性能 控制性能
控制性能 控制性能
控制性能指回響從終值 上升到終值 所需的時間;對於有振盪的系統,也可定義為回響從零第一次上升到終值所需的時間。上升時間 是系統回響速度的一種度量。上升時間越短,回響速度越快。
峰值時間t
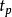 控制性能
控制性能指回響超過其終值達到第一個峰值所需的時間。上升時間是系統回響速度的一種度量。
調節時間(settingtime)t
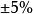 控制性能
控制性能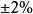 控制性能
控制性能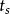 控制性能
控制性能指回響到達並保持在終值(或)內所需的最短時間。調節時間是評價系統回響速度和阻尼程度的綜合指標。
超調量(overshoot):σ%
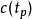 控制性能
控制性能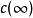 控制性能
控制性能指回響的最大偏離量與終值之比的百分數,即
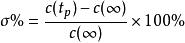 控制性能
控制性能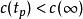 控制性能
控制性能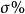 控制性能
控制性能若,則回響無超調。評價系統的阻尼程度。
穩態指標
(1)穩態過程
穩態過程指系統在典型輸入信號作用下,當時間t趨於無窮時,系統輸出量的表現方式。穩態過程又稱為穩態回響,表征系統輸出量最終復現輸入量的程度,提供系統有關穩態誤差的信息,用穩態性能描述。
(2)穩態性能——穩態誤差(steady-state error)
穩態誤差是描述系統穩態性能的一種性能指標,通常在階躍函式、斜坡函式或加速度函式作用下進行測定或計算。若時間區域無窮時,系統的輸出量不等於輸入量或者輸入量的確定函式,則系統存在穩態誤差。穩態誤差是系統控制精度或抗擾動能力的一種度量。
