簡介
指標理論是疇數理論在T(G)不變泛函情形的變種形式。
設G是緊拓撲群，X是T(G)空間，∑={A⊂X|A是T(G)不變閉集}。若函式i:∑→Z∪{+∞}滿足下述條件：
1、平凡性。i(A)=0⇔A=∅。
2、單調性。A,B∈∑，A⊂B⇒i(A)≤i(B)。
3、次可加性。∀A,B∈∑，i(A∪B)≤i(A)+i(B)。
指標理論4、超變性。若A∈∑，h=η(∙,1)，η:[0,1]×X→X是T(G)等變形變，則。
5、連續性。若A∈∑，A緊，則存在A的某個閉鄰域N∈∑，使得i(N)=i(A)，則稱i為X上的一個T(G)指標。
規範指標
若指標i還具有性質：
6、規範性。∀p∈X。若[p]∩Fix=∅，則i([p])=1，其中[p]={Tp|g∈G}，Fix={x∈X|Tx=x,∀g∈G}，則稱指標i是規範的。
性質
若存在正整數d，使對X的dk維T(G)不變子空間V (k=1,2,...)，只要V ∩Fix={0}，就有i(V ∩S)=k，其中S為X中的單位球面，則稱指標i具有d維數性質。
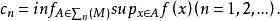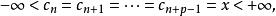指標理論
指標理論類似於疇數理論，有下述指標意義下的重數定理：設M是X中的不變閉子流形，f∈C (M,R)滿足(P.S)條件，i是X上的T(G)指標，記∑n(M)={A∈∑|A⊂M,i(A)≥n}。令若對某正整數n與p，有則c是f的臨界值，且i(K)≥p。這時如果i是規範的，且K∩Fix=∅，則K中至少含有p條不同點的臨界點軌道。
最常用到的指標是G=Z與G=S 時的情形。作為指標概念的推廣或變種，尚有偽指標、相對指標等多種概念。
