指數型母函式

普通型母函式主要是來求組合的方案數，而指數型母函式是求多重排列數。

問題引出

指數型母函式問題：
假設有n個元素，其中a1，a2，····，an互不相同，進行全排列，可得n!個不同的排列。若其中某一元素a1重複了n1次，全排列出來必有重複元素，其中真正不同的排列數應為n!/n1!，即其重複度為n1!

同樣理由a1重複了n1次，a2重複了n2次，····，ak重複了nk次，n1+n2+····+nk=n。對於這樣的n個元素進行全排列，可得不同排列的個數實際上是

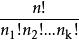指數型母函式

定義

對於序列a0，a1，a2，····定義

指數型母函式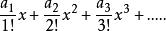

指數型母函式

Ge(x)= +

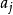指數型母函式

為序列{ }的指數型母函式

舉例：

設n是正整數。確定下列數列的指數生成函式：

p(n,0),p(n,1),p(n,2),…,p(n,n)

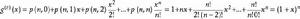指數型母函式

其中p(n,k)表示n元素的k排列的數目，因此對於k=0,1,2,…,n，這個排列的數目是n!/(n-k)!。因此指數生成函式是：

因此 是數列p(n,0),p(n,1),p(n,2),…,p(n,n)的指數生成函式。