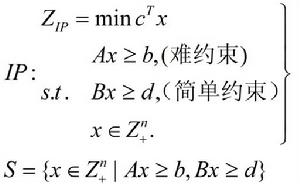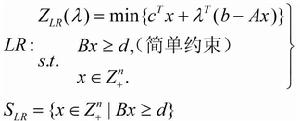拉格朗日鬆弛技術

簡介

拉格朗日鬆弛技術（Lagrangian relaxation technique）
拉格朗日鬆弛技術是用以求解約束規劃的一種數學方法。

算法最佳化的鬆弛技術

在實際計算中常常可以獲得目標值F*的兩個相伴隨的近似值F0與F1，為將其加工成精度更高的結果，取二者的某種加權平均值作為改進值，適當選取權係數來調整校正量，正是由於這種基於校正量的調整與鬆動，稱之為鬆弛技術。

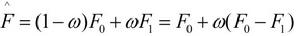對原有值進行改進的鬆弛技術

拉格朗日鬆弛方法

基本原理

將目標函式中造成問題難的約束吸收到目標函式中，並保持目標函式的線性，使問題更加容易求解。

最佳化目的

在一些組合最佳化中，在原問題中減少一些約束，使得問題的求解難度大大降低（稱這類約束為難約束）。

基於規劃論的鬆弛方法

給定整數模型：

當問題RP：

滿足下列性質時，稱為原整數規劃問題的一個鬆弛（relaxation）:
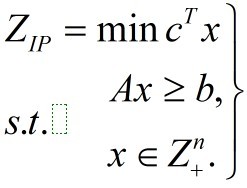
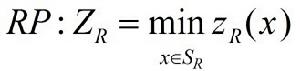
1.可行解區域兼容：其中S為原整數規劃問題的可行域

2.目標函式兼容：

拉格朗日鬆弛理論

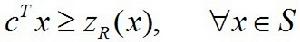
當原整數規劃問題為：

拉格朗日鬆弛即為：