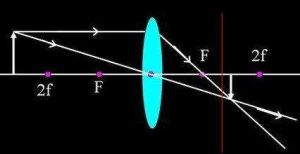
推導方法
凸透鏡的成像規律是1/u+1/v=1/f(即:物距的倒數與像距的倒數之和等於焦距的倒數。)一共有兩種推導方法 。分別為“幾何法”與“函式法”
幾何法
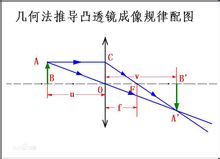
【題】如右圖 ,用幾何法證明1/u+1/v=1/f。
【解】∵△ABO∽△A'B'O
∴AB:A'B'=u:v
∵△COF∽△A'B'F
 成像公式
成像公式∴CO:A'B'=f:(v-f)
∵四邊形ABOC為矩形
∴AB=CO
∴AB:A'B'=f:(v-f)
∴u:v=f:(v-f)
∴u(v-f)=vf
∴uv-uf=vf
∵uvf≠0
∴(uv/uvf)-(uf/uvf)=vf/uvf
∴1/f-1/v=1/u
即:1/u+1/v=1/f
函式法
 成像公式
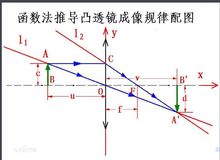
成像公式【題】 如右圖 ,用函式法證明1/u+1/v=1/f。
【解】一基礎
右圖為凸透鏡成像示意圖。
其中c為成像的物體長度,d為物體成的像的長度。u為物距,v為像距,f為焦距。
步驟
(一)為便於用函式法解決此問題,將凸透鏡的主光軸與平面直角坐標系的橫坐標軸(x軸)關聯(即重合),將凸透鏡的理想折射面與縱坐標軸(y軸)關聯,將凸透鏡的光心與坐標原點關聯。則:點A的坐標為(-u,c),點F的坐標為(f,0),點A'的坐標為(v,-d),點C的坐標為(0,c)。
(二)將AA’,A'C雙向延長為直線l1,l2,視作兩條函式圖象。由圖象可知:直線l1為正比例函式圖象,直線l2為一次函式圖象。
(三)設直線l1的解析式為y=k1x,直線l2的解析式為y=k2x+b
依題意,將A(-u,c),A'(v,-d),C(0,c)代入相應解析式得方程組:
c=-u·k1
-d=k2v+b
c=b
把k1,k2當成未知數解之得:
k1=-(c/u)k2=-(c/f)
∴兩函式解析式為:
y=-(c/u)x y=-(c/f)x+c
∴兩函式交點A'的坐標(x,y)符合方程組
y=-(c/u)x
y=-(c/f)x+c
∵A'(v,-d)
∴代入得:
-d=-(c/u)v
-d=-(c/f)v+c
∴-(c/u)v=-(c/f)v+c=-d
∴(c/u)v=(c/f)v-c=d
cv/u=(cv/f)-c
fcv=ucv-ucf
fv=uv-uf
∵uvf≠0
∴fv/uvf=(uv/uvf)-(uf/uvf)
∴1/u=1/f-1/v
即:1/u+1/v=1/f
實際運用
人眼
人類的眼睛所成的像,是實像還是虛像呢?我們知道,人眼的結構相當於一個凸透鏡,那么外界物體在視網膜上所呈的像,一定是實像。根據上面的經驗規律,視網膜上的物像似乎是倒立的。可是我們平常看見的任何物體,明明是正立的啊?這個與經驗與規律發生衝突的問題,實際上涉及到大腦皮層的調整作用以及生活經驗的影響。由於視覺錯誤,人眼認為光是由物體發出並直射入人眼。
當物體與凸透鏡的距離大於透鏡的焦距時,物體成倒立的像,當物體從較遠處向透鏡靠近時,像逐漸變大,像到透鏡的距離也逐漸變大;當物體與透鏡的距離小於焦距時,物體成放大的像,這個像不是實際折射光線的會聚點,而是它們的反向延長線的交點,用光屏接收不到,是虛像。平面鏡所成的虛像對比(不能用光屏接收到,只能用眼睛看到)。
照相機
照相機的鏡頭就是一個凸透鏡,要照的景物就是物體,膠片就是螢幕。照射在物體上的光經過漫反射通過凸透鏡將物體的像成在最後的膠片上;膠片上塗有一層對光敏感的物質,它在曝光後發生化學變化,物體的像就被記錄在膠捲上
而物距、像距的關係與凸透鏡的成像規律完全一樣。物體靠近時,像越來越遠,越來越大,最後再同側成虛像。物距增大,像距減小,像變小;物距減小,像距增大,像變大。一倍焦距分虛實,二倍焦距分大小。
其他
放映機,幻燈機,投影機,放大鏡,探照燈,攝像機和攝像頭都套用了凸透鏡,凸透鏡完善了我們的生活,時時刻刻都套用在生活中。遠視眼鏡就是凸透鏡,近視眼鏡就是凹透鏡。
另外凸透鏡還用於:
1、拍攝、錄像
2、投影,幻燈,電影
3、用於特效燈光(聚焦成各種花色)
4、成虛像用於放大文字、工件、地圖等