內容簡介
如果一開始就能把握對微積分的基本認識，你會發現不用記憶太多的公式，思考問題的方法卻變得越來越簡單。保證誰都能理解它，誰都會覺得有趣，在體驗其樂趣和奧妙的同時，慢慢習慣用它來思考問題吧！
本書正如書名所示，是微積分的超入門書。本書的目標讀者群是對微積分感興趣的讀者，將要學習微積分的高中生，還有進入大學後必須學習微積分的大學生（如經濟系的學生），就職後感覺有必要掌握金融業等領域微積分知識的人……總之，不管過去有無學過微積分，不管現在對微積分是否有印象，即使是“現在有關微積分的認識、想法幾乎是等於零”，都可以讀懂這本書。
作品目錄
第一章
形象認識微分與積分
微積分超入門1 動畫——微分與積分的第一印象
2 “連續變化”是怎樣的變化
3 平均速度VS瞬時速度
4 如何求瞬時速度
5 從地圖的面積著手了解積分
6 面積是線段的集合嗎
7 微分與積分到底是什麼
專欄1 《林德紙草書》的數學
第二章
初探極限世界
1 騎士能到達城堡嗎——最大限度的概念
2 0.9999…=1嗎
3 以分數表示循環小數
4 阿喀琉斯能追上烏龜嗎
5 極限值=收斂
專欄2 飛矢不動？
第三章
通往微分之路：曲線的初線
1 切線是什麼
2 追蹤賽車方向
3 圓的弦的極限就是切線
4 曲線尖頭部位畫不出切線
5 變化的比例
6 平均變化率和弦的斜率
7 瞬間的弦的斜率=切線的斜率
8 “微分係數”是微分的根本原理
9 求出切線的方程
專欄3《九章算術》的體積計算
第四章
有曲線可“微分”
1 饅頭和函式
2 微分係數太麻煩，使用“導函式”吧
3 微分運算（1）——二次函式的運算是基礎
4 微分運算（2）——直線和常數的情況
5 使用“微分公式”立刻得出答案
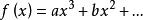微積分超入門6 微分函式
7 記憶更複雜的微分公式
8 微分練習
專欄4 天才關孝和和圓周率
第五章
掌握微分公式，順利解題
1 切線的斜率道出了“曲線的形狀”
2 曲線的升降——單調遞增與單調遞減
3 局部的最大和最小——極大值、極小值
4 通過圖表描繪出曲線的大致形狀——掌握函式增減表
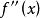微積分超入門5 判斷曲線凹凸的方法——求二次微分的正負
6 懂得增減、極值、凹凸，就可完全掌握圖像
7 三次函式的圖像是怎樣的
8 三次函式可以作幾條切線
10 肥皂泡的膨脹速度
專欄5 最快的旋輪線曲線
第六章
積分是微分的逆運算嗎
1 求原函式
2 這就是積分公式
3 是先積分後微分，還是先微分後積分
4 從切線的斜率求原來的函式
5 定積分中“C”消失了
6 積分練習
專欄6 通過積分預測“櫻花前線”
第七章
掌握積分
1 微小的變化決定全體（1）——求圓的面積
2 微小的變化決定全體（2）——測量側面的水壓
3 利用定積分計算面積——曲線所成面積
4 二次函式所形成的面積
5 可以將面積認為是“積分的和”嗎
6 求兩條曲線圍成的區域面積
7 以定積分求面積——微積分學的基本原理
8 體積是面積的和——阿基米德的主張
9卡瓦列里原理——截面積比一定時，體積比也與之相同
10 來切切蘿蔔——以積分求體積
11 圓錐的體積公式——為什麼是圓柱體積的三分之一
12 斜切圓柱所得體積
13 旋轉圓，得到球——切面總為圓
專欄7 “微積分的創始人”之間關係惡劣？
第八章
得心應手使用微分與積分
1 用積分求極值的差——微積分的基本定理的套用
2 正方形的n分之一的面積——用拋物線3等分
3 年輪形點心（圓柱體）的體積——“圓柱形薄膜”的集合
4 求圓環體的體積——Guldin（古魯金）定理
5 削蘋果皮——微分使得“次數”下降
6 關於微分方程——用積分來解
7 蘋果自由下落——推導出萬有引力定律
8 往往返返的距離——用面積求距離
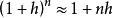微積分超入門9 用“近似計算”快速求解——利用
專欄8 微分方程不可解？
