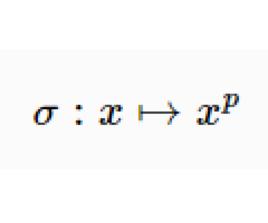基本介紹
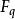 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構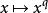 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構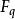 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構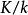 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構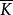 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構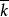 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構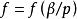 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構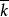 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構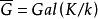 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構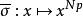 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構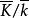 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構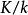 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構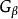 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構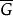 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構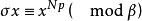 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構弗羅貝尼烏斯自同構是(數)域的一種特殊自同構,q元有限域 的擴域中,由 確定的自同構稱為 弗羅貝尼烏斯自同構。其他的由升q次冪確定的自同構(如 上曲線)也這樣稱呼。設 為數域伽羅瓦擴張,p為k的素理想,β為其在K的素理想因子,K模β的剩餘類域 是 的 次擴張, 是 (即p的絕對範數)個元素的有限域,伽羅瓦群 是循環群,生成元 稱為 的 弗羅貝尼烏斯自同構。 的保持β不變的自同構群 到 有自然同態,在此同態下的任一原像稱為β的弗羅貝尼烏斯自同構σ,由 刻畫 。
相關概念
有限域
有限域又叫做伽羅瓦域,是由伽羅瓦首先提出而得名的,有限域的特徵顯然只能是素數,它是一類很重要的域,它有很好的性質而且還有很重要的套用。
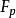 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構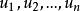 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構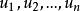 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構設K為一個特徵p的有限域,於是K包含 作為子域,K自然地可以看成 上的有限維線性空間,設K對 的維數為n, 為它的一基,於是K的每個元素 可以唯一地表成 的線性組合
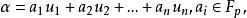 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構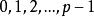 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構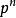 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構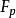 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構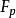 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構可以獨立地取 ,因而K恰由 個元素組成。因而這對K的基數作出了規定,K的基數只能是它的特徵的一個方冪,冪指數等於K對 的維數,也是K對 的次數。
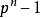 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構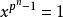 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構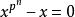 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構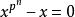 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構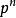 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構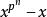 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構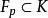 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構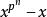 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構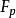 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構其次, K的全部非零元素K*組成一個 階乘法群,根據拉格朗日定理, K*的每個元素都是方程 的根,因而K的每個元素都是 的根,但是 在K內最多有 個根,所以K的元素恰好是 的全部根,由於 可知K是 在 上的分裂域,這就證明下列定理的唯一性部分。
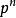 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構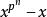 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構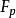 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構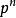 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構定理1 對每個素數p和任一正整數n,存在一個唯一的 個元素的有限域,它就是 在 上的分裂域,除此之外無其它 個元素的有限域。
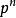 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構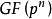 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構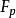 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構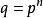 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構個元素的有限域習慣記成 或 , 。
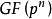 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構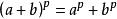 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構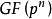 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構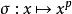 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構最後指出有限域 有一個很重要的自同構即 弗羅貝尼烏斯(Frobenius)自同構,利用特徵p>0的域的一條性質 ,作一個 到自身的映射 , 滿足
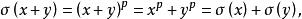 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構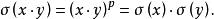 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構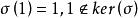 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構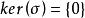 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構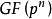 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構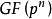 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構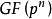 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構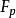 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構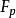 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構因而 是一個自同態。其次, 是單的。這是因為 ,所以 ,即 單。由於 有限,單射必然是滿的。所以 是 的一個自同構。它叫做 的 弗羅貝尼烏斯自同構。 顯然保持 的元素不動,因而 是一個 -自同構。
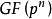 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構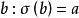 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構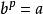 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構作為弗羅貝尼烏斯自同構的一個推論, 的每個元素 可以開p次方。因為 是滿射, 在 下有一個原象 ,即 ,所以b是 的一個p次方根。由於 的單一性, 的p次方根是唯一的 。
分圓函式域
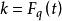 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構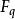 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構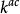 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構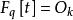 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構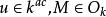 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構分圓函式域(cyclotomic function field)是一類重要的代數函式域,是分圓數域的某種推廣。設 為有限域 上單變元t的有理函式域,其代數閉包 按如下作用形成 上的模:對 ,定義
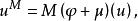 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構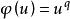 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構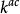 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構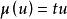 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構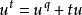 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構式中 是 的 弗羅貝尼烏斯自同構, ,特別地, ,於是
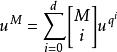 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構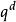 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構是次u的可分多項式,式中d為M的次數,
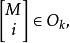 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構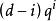 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構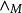 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構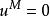 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構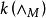 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構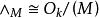 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構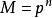 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構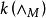 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構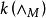 弗羅貝尼烏斯自同構
弗羅貝尼烏斯自同構次數為,若為的根集,則稱為M分圓函式域,其在k上的伽羅瓦群同構於的單位群,當為d次首一不可約多項式冪時,僅在(P)和∞分歧,類似於克羅內克-韋伯定理,k的每個在∞為順分歧的有限阿貝爾擴張均含於某個分圓函式域的常數域擴張中(順分歧是指分歧指數與q互素) 。