基本介紹
設n≥2，a，a，…，a都是正整數，(a，a，…，a)=1，再設x≥0 (i=1，2，…，n)的線性型ax+ax+…+ax不能表出的最大整數為g(a，a，…，a)，即對大於它的任意整數m，存在整數x≥0 (i=1，2，…，n)，使ax+ax+…+ax=m，研究g(a，a，…，a)的存在性及其解法，就是關於丟番圖方程ax+ax+…+ax=c的 弗羅貝尼烏斯問題 。
該問題不僅在不定方程理論上有重要意義，還在規劃論、計算技術、合理下料、合理派工等方面都有實際套用。對此問題，目前研究的結果為：當n=2時，g(a，a)=aa-a-a；在n≥3時，關於g(a，a，…，a)尚無一般表示式，但在多種情形已有些不同的方法。例如，當a>aa/(a，a) -(a+a)/(a+a)時，可算得g(a，a，a)=aa/(a，a)+a(a，a)-a-a-a，由於g(a，a，a)=g(a，a，a)=g(a，a，a)，上麵條件及結果中的a，a，a可以輪換，對於一般的n有
弗羅貝尼烏斯問題其中d=(a，a，…，a) (i=2，3，…，n)，d=a(d=1) 。
相關證明
n=2時，易知所求的數為aa-a-a證明如下 ：
首先，設m>aa-a-a方程
弗羅貝尼烏斯問題的全部解可寫成
弗羅貝尼烏斯問題
弗羅貝尼烏斯問題
弗羅貝尼烏斯問題其中是(1)的任一組整數解，t為任意整數。可以假定0≤x₂<a (否則將x₂加上或減去若干個a₁)，這時
弗羅貝尼烏斯問題
弗羅貝尼烏斯問題
弗羅貝尼烏斯問題因此，x₁≥0，即m=ax+ax，x，x都是非負整數 。
另一方面，若
弗羅貝尼烏斯問題其中x，x為非負整數，則
弗羅貝尼烏斯問題
弗羅貝尼烏斯問題從而。
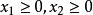弗羅貝尼烏斯問題
弗羅貝尼烏斯問題因為，所以從而
弗羅貝尼烏斯問題矛盾。
所以，aa-a-a是不能表示成ax+ax(x，x為非負整數)的最大整數。
n=3的情況，直至1978年才由E.S.Selmer與Ö.Beyer利用連分數給出有顯表達式的解答，同年O.J.Rodseth對他們的解答作了簡化，1988年，H.Greenberg進一步作了簡化，使所用步驟量為O(log a)。
n≥4時，尚無一般公式 。
