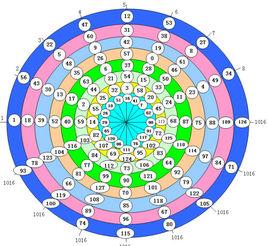
楊輝幻圓
楊輝《續古摘奇算法》有聚五圖、聚六圖、聚八圖、攢九圖、八陣圖、連環圖 。
攢九圖
楊輝《續古摘奇算法》中的 攢九圖以自然數1至33構成，9在圓心，其餘排列在四個同心圓上，每圈8個數。楊輝有如下攢九圖奇妙特點：
1）四條直徑上數字之和是147，
28+5+11+25+9+7+19+31+12=147
2）四個圓周上數字之和加圓心9之和也是147。
28+27+20+33+12+4+6+8+9=147
3）八條半徑線上數字（不包括9）之和=69
27+15+3+24=69
4）四個圓周上數字之和（不包括9）=八條半徑線上數字和的兩倍。
圖1.南宋楊輝幻圓包含的幻數“69”多達16個圖的構造
楊輝書中未曾說明幻圓的構造方法。新加坡大學藍麗蓉教授建議將八組半徑數字分為兩組，構成兩個四階幻方，例如：
幻圓
幻圓由於這兩個四階幻方縱數橫數之和都是69，只需從第一幻方和第二幻方中隨意各取一行，或隨意各取一列，構成同一條直徑上的兩對半徑，一共組成四條直徑，每直徑8個數，最後在圓心安方9，就不但可以排出楊輝幻圓；而且可以排除許許多多不同排列的幻園。此外，由於數字的和與數字的次序無關，因此：
•任何兩組半徑數字，可以互換位置，
•8組半徑數字，在可以在圓圈上任意排列，
•任何兩組園圈，可以互換位置。
楊輝幻圓真是富於變化。如果限制四個圓周上必須有兩個同和半圓(半圓上的四個數字之和必須=69)，楊輝幻圓上的半徑位置就不可調換。如此一來，楊輝幻圓可以有
•8條同和半徑；28+5+11+25=69，20+16+23+10=69，……
•8條同和半圓； 27+28+8+6=69，20+33+12+4=69,15+5+17+32=69，21+32+1+16=69……
具有16個同和線段（和數為69）的幻圓不止一個，可依靠四個圓圈的不同排列得到，共有4x3x2=24種。
楊輝八陣圖
1至64， 64數字分為八個圓圈，每個圓圈內數目之和=260。 從西北角順時針方向各小圓之和為：
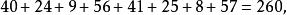幻圓
幻圓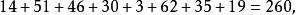
幻圓
幻圓
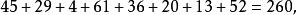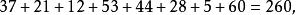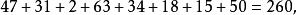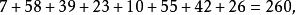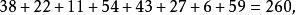幻圓
幻圓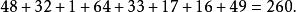
幻圓
幻圓又東西方向和南北方向的八個數字之和也是260：
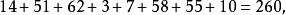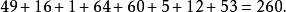幻圓
幻圓此外兩條對角線的16個數字之和為260的兩倍：
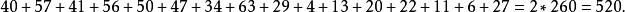幻圓
圖2.楊輝八陣圖楊輝連環圖
1至72，共72個數字分為9個圓圈，排列成方陣如圖。
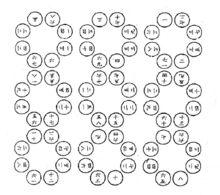圖3.楊輝連環圖此連環圖奇妙之處在於連環生圈：由於左右相鄰的四個圈的數字連環，又多出4 8字圓圈連環圈。由有以下相鄰的8字圈連環組成：
（東北，北，東，中），
（西北，北，西，中），
（東南，南，東，中），
（西南，南，西，中）。
1.（東北，北，東，中），
2.（西北，北，西，中），
3.（東南，南，東，中），
4.（西南，南，西，中）。
一共13個八字圈： ：西北，北，東北，東，東南，南，西南，西，中，（東北，北，東，中），（西北，北，西，中），（東南，南，東，中），（西南，南，西，中）。
13個八字圈中任何一個八字圈的數字之和=292，
橫向三個八字圈24個數字之和=876，
縱向三個八字圈24個數字之和=876，
對角線上三個八字圈24個數字之和=876。
1.13個八字圈中任何一個八字圈的數字之和=292，
2.橫向三個八字圈24個數字之和=876，
3.縱向三個八字圈24個數字之和=876，
4.對角線上三個八字圈24個數字之和=876。
丁易東幻圓
南宋數學家丁易東是楊輝同時代人，以自然數1至49作出六同心圓幻圓，稱之為太衍五十圖 。丁易東幻圓特性：
1）各圓周數字之和為200
3+4+49+2+47+46+1+48=200；
13+14+39+12+37+36+11+38=200；
……
2）每圓周上的一個數與其相對點上數字之和=50；
3+47=50，13+37=50……
3）四條直徑上數字之和為325
據上條，6x50+25=325。
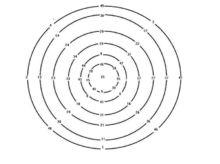圖4.南宋丁易東太衍五十圖幻圓構造
丁易東給出把三階幻方洛書變化為六階幻園 太衍五十圖的的奇妙方法；
將從1至49的數字分成以下9組：
1）凡個位數為1數按大小次序排為一組：1，11，21，31，41，
2）凡個位數為2數按大小次序排為一組：2，12，22，32，42，
3）凡個位數為3數按大小次序排為一組：3，13，23，33，43，
4）凡個位數為4數按大小次序排為一組：4，14，24，34，44，
5）凡個位數為6數按大小次序排為一組：6，16，26，36，46，
6）凡個位數為7數按大小次序排為一組：7，17，27，37，47，
7）凡個位數為8數按大小次序排為一組：8，18，28，38，48，
8）凡個位數為9數按大小次序排為一組：9，19，29，39，49，
9）5及其倍數按大小次序排為一組：5，10，15，20，25，30，35，40，45。
按洛書口訣：“戴九履一，左三右七，二四為肩，六八為足”排列數字組：
戴九：將“9字組”9，19，29，39，49 排在最頂部，49在上，循序循半逕往下排列，
履一，將“1字組”1，11，21，31，41作履，1排在最下，循序循半逕往上排列，
左三：將“3字組"3，13，23，33，43排在左邊，
右七，將“3字組"：7，17，27，37，47排在右邊，
二四為肩，將“2字組”2，12，22，32，42，“4字組”4，14，24，34，44按絡書方位排列在左上右上。
六八為足：將“6字組”6，16，26，36，46，“8字組”8，18，28，38，48按絡書方位排列在左下右下。
最後“5”字組5，10，15，20，25，30，35，40，45各數對應其1/5的數字組排列在最內一個圓上：1）5的1/5=1，排在“1字組”；
2）10的1/5=2，排在“2字組”……
1.戴九：將“9字組”9，19，29，39，49 排在最頂部，49在上，循序循半逕往下排列，
2.履一，將“1字組”1，11，21，31，41作履，1排在最下，循序循半逕往上排列，
3.左三：將“3字組"3，13，23，33，43排在左邊，
4.右七，將“3字組"：7，17，27，37，47排在右邊，
5.二四為肩，將“2字組”2，12，22，32，42，“4字組”4，14，24，34，44按絡書方位排列在左上右上。
6.六八為足：將“6字組”6，16，26，36，46，“8字組”8，18，28，38，48按絡書方位排列在左下右下。
7.最後“5”字組5，10，15，20，25，30，35，40，45各數對應其1/5的數字組排列在最內一個圓上：1）5的1/5=1，排在“1字組”；
2）10的1/5=2，排在“2字組”……
