幅角原理

幅角原理是關於解析函式在簡單閉曲線內部的零點個數與極點個數之間的關係的定理。幅角原理是複變函數中的原理，是奈氏判據的數學基礎， 幅角原理用於控制系統的穩定性的判定還需選擇輔助函式和閉合曲線。

簡介

幅角原理是關於解析函式在簡單閉曲線內部的零點個數與極點個數之間的關係的定理。

設Γ為一簡單閉曲線，函式f(z)滿足條件：

1、f(z)在Γ的內部除有有限個極點外是解析的；

2、f(z)沿Γ上解析且不為零；

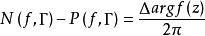幅角原理

則f(z)在簡單閉曲線Γ內部的零點與極點個數之差，等於z沿Γ之正向繞行一周時，argf(z)的改變數△argf(z)除以2π，即，這裡N(f,Γ)和P(f,Γ)分別表示f(z)在Γ內部的零點個數和極點個數。

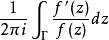幅角原理

註：上式右端的量可寫成積分（對數留數）。

結論

設s平面閉合曲線Γ包圍F(s)的Z個零點和P個極點，且不經過這些零極點，則s沿Γ順時針運動一周時，在F(s)平面上，有閉合曲線Γ包圍原點的圈數R=Z-P，其中R>0和R<0分別表示Γ順時針包圍和逆時針包圍F(s)平面的原點，R=0表示不包圍F(s)平面的原點。

套用

複變函數中的幅角原理是奈氏判據的數學基礎， 幅角原理用於控制系統的穩定性的判定還需選擇輔助函式和閉合曲線。