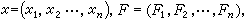常微分方程攝動方法

一般的微分方程,常常不能求得精確解析解,需要藉助於求近似解或數值解,或兩者兼而有之。攝動方法是重要的近似方法。它的思想,在於構想有可能藉助於選定的並且具有精確解的微分方程組，用來逐次近似地描述所研究的微分方程。常見的是含有小參數ε的微分方程。

正文

例如凧=F(x,t,ε),其中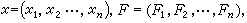
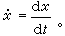ε是小參數。 所謂攝動方法，就是根據方程凧=F(x0,t,0)的已知解,求得原式當ε 取小值時的近似解的方法。一般假定F(x,t,ε)於ε=0時有意義，並且對ε是解析的,這是正則攝動問題。如果F(x,t,ε)於ε=0時出現奇性（包括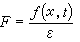的情形），則為奇異攝動問題。或者廣義地說,若攝動問題Pε的解uε(x)能用ε的漸近冪級數表示，即：
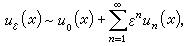並且這一漸近冪級數在所討論的區域內一致有效成立，則稱Pε是正則攝動問題,否則稱為奇異攝動問題，其中u0(x)是ε=0時非攝動問題（或稱退化問題）的解。對正則攝動問題，可利用方程和定解條件逐次確定係數ui(x)(i>0)，而對奇異攝動問題，則不然。
正則攝動　關於正則攝動問題有下面幾種常用的方法。
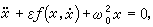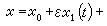
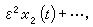① 林斯泰特－龐加萊方法　它原用於天體力學。例如對方程： 設其中 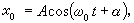當 A,α是常數時，它是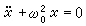的解。若直接以x的式子代入方程，並使ε的各次冪的係數分別為零，以求(x)i(t),便會得到形如tmsin(nω 0t)及tmcos(nω 0t)的項，即所謂長期項(也稱永年項),長期項的出現大大妨礙了級數於t→時的收斂。為了避免長期項的出現，A.林斯泰特首先提出，後由H.龐加萊補充完善,得到所謂林斯泰特-龐加萊方法（簡稱LP方法）。其技巧在於選用x0=Asin(ωt+α)，將頻率ω 展開成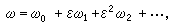對自變數t作線性變換τ=ωt,並在新自變數τ下展開 x(t),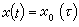+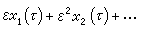代入方程以確定xi(t)，與此同時, 為可選取參數 ω1,ω2,…,消除長期項。但這個方法對於消除一些問題中高階近似的強奇性是無效的。1949年，M.J.萊特希爾作了重要推廣，引進了自變數的非線性變換，求得了一系列物理問題的一致有效漸近解。
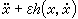
② 克雷洛夫-博戈柳博夫方法　在方程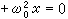中，如令ε=0，則得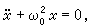其通解為x=Acos(ω0t+α)，A，α 為常數。當│ε│很小且不為零時，設A、α為t的函式，並令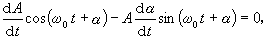　

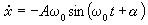
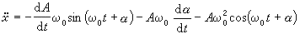
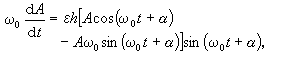
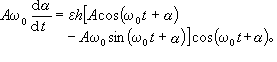
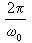則有

代入原方程連同所令關係式可解出

由於這兩個式子右邊都是以ε 為因子的項和t 的周期函式，故A、α是t的慢變數。因此可取它們對周期的平均值，經過整理和變數變換 (u=ω0t+α)，可得到確定A、α的兩個近似方程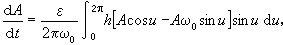

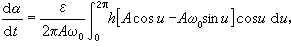
由此，可求得A、α為t 的函式。由於取了函式的平均值，此法又稱平均法。
一般情況，方程化成凧 ＝εΧ（x,凧,t），如果Χ對t是周期為T 的函式，可取 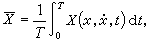或存在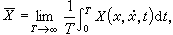則在某些條件下，近似方程是 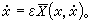解之即得近似解。
③ 調和均衡法　這是將 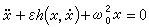的εh(x,凧)調和線性化，即若εh(x,凧)=mx+n凧+…，取前兩項把原式化成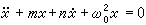

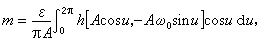
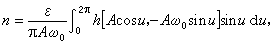
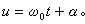
其中



亦即，當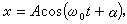而A、α、ω0都是常數的情況下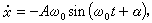，h是t的周期函式。
奇異攝動　關於奇異攝動問題，不能直接用非攝動問題(ε=0) 的解在所討論的區域內得到一致有效的漸近解，即正則攝動方法對奇異攝動問題是無效的。常微分方程奇異攝動問題主要是大參數問題。下面列舉兩種類型問題。
第一類，場函式和它的各階導數不是同量級量的問題。這時小參數ε(ε>0)含於微分方程的高階導數項，當ε=0時，方程降階，定解條件過剩,為了使退化問題可解，必須丟掉一部分定解條件。在丟掉定解條件的那一部分邊界附近（物理上稱為邊界層區域），攝動問題的解變化很快，當 ε→0 時其解不能一致收斂於退化問題的解。例如，考慮初值問題 Lεuε＝εu┡+u＝1，u(0)＝0，或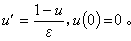其精確解為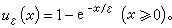
當ε→0時其極限函式ū(x)為

在點x=0,uε(0)=0,而u夊(0)=1/ε。如用正則攝動法求其漸近解堚ε(x)=u0(x)+εu1(x)+…，則堚ε(x)=1。顯然是錯誤的。
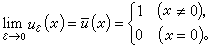
第二類，在微分方程的係數中具有轉向點的奇點問題。例如, 方程u″+λ2(1-x2)u=0,其中λ是大參數（或寫成 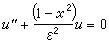,這裡,ε是小參數）。此時方程的解當│x│<1時表現為振盪型的，當│x│>1時表現為指數型的（發散的或衰減的）。 x=±1稱為轉向點。在轉向點附近解急劇變化，用正則攝動法求得的漸近解將在轉向點產生奇性，非一致有效。
處理上述問題的方法稱為奇異攝動方法。自1935年以來它有了很大發展，成為套用數學中的一個重要領域。對於第一類邊界層型奇異攝動問題有匹配法，邊界層校正法（又稱合成展開法）和多重尺度法。對於轉向點問題有由G.文策爾、H.A.克拉默斯和L.N.布里尤安於1926年各自獨立地提出的方法，後來稱之為WKB方法,和先後由R.E.蘭格(1931、1934)和F.W.J.奧爾弗(1954)發展起來的LO方法以及B.∏.馬斯洛夫提出來的方法(1965)。
近十多年來，研究奇異攝動問題的數值方法也有了發展,根據奇異攝動問題的特點構造特殊的數值方法(有限差分方法和有限元方法) ，以便取得良好的數值結果。
中國力學工作者在對攝動方法的發展有開創性貢獻。錢偉長在1948年解圓板大撓度問題時，即提出現在稱為合成展開法的方法，郭永懷在1953年把由龐加萊和萊特希爾發展起來的方法推廣套用於邊界層效應的粘性流問題；錢學森1956年又深入闡述了這個方法的重要性，並稱之為PLK方法。
參考書目
　A. H. Nayfeh,Perturbation Methods, John Wiley & Sons,New York, 1973.
　R.E.O'Malley,Introduction to Singular Perturbations,Academic Press, New York, 1974.
　Tsien Hsue-Shen,The Poincare-Lighthill-Kuo Method,Advan. Appl. Meth.,4, pp. 281～349,1956.