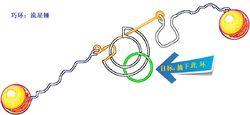
 巧環
巧環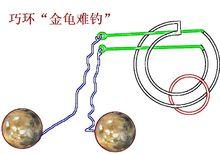 巧環
巧環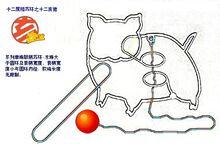 中國古典智力玩具-十二生肖系列巧環賞析
中國古典智力玩具-十二生肖系列巧環賞析 合併圖冊
合併圖冊關於巧環
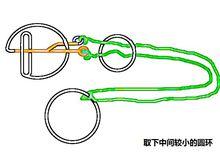 巧環
巧環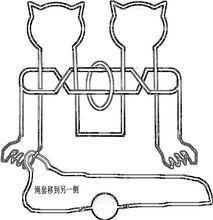 巧環
巧環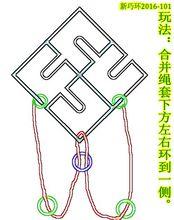 巧環
巧環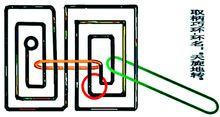 巧環
巧環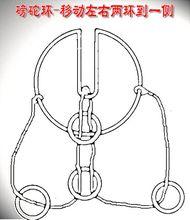 巧環
巧環 巧環
巧環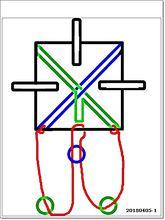 巧環
巧環 2018
2018按遊戲目的可分為:取柄環、解繩環、移珠環、並繩等等。 1958年俞崇恩出版《巧環》,收錄蘇州阮氏巧環24種,1999年再版時更名為《千變萬化的九連環》。
2000年周偉中出版《九連環圖譜》,2003年又出版《巧解九連環》,收錄巧環60餘種,並對巧環做了詳細的分類和研究。
2003年王宗一出版《神秘的繩套》,收錄巧環50種。以及《中國七巧環》(作者陳乃斌著,中國文化遺產,瀕臨失傳)
 巧環
巧環 巧環
巧環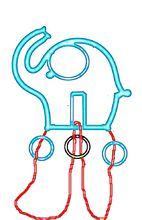 巧環
巧環另外還有:
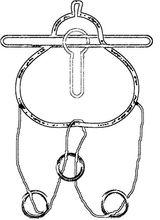 穿越與合併-巧環-鴨梨山大
穿越與合併-巧環-鴨梨山大大型巧環電子書《巧環之春》(憂天杞人編著)。
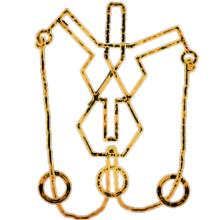 新巧環圖冊
新巧環圖冊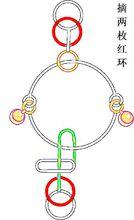 巧環
巧環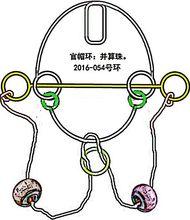 巧環
巧環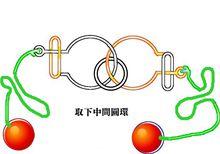 拳套巧環三部曲
拳套巧環三部曲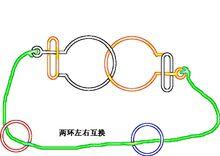 巧環
巧環 天螺環
天螺環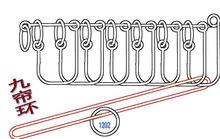 九簾環
九簾環專輯電子書圖籍 <從珠連璧合到完璧歸趙>
 巧環
巧環 巧環
巧環以九連環為代表的連環類智力玩具起源於中國,相傳它是根據古代貴重俯地,機關門鎖的原理改進過來,且流傳千年而不衰,曾征服了古今中外無數愛好者,是中華民族傳統文化中的一顆璀璨的明珠。連環類智力玩具的魅力在於它的神秘性、挑戰性和品種的多樣性。具有較強的趣味性,有助於啟迪人們的智慧、並對開發智力很有益處。
九連環流行極廣,形式多樣,規格不一。其製作,用金屬絲製成圓形小環九枚,九環相連,套在條形橫板或各式框架上,其框柄有劍形、如意形、蝴蝶形、梅花形等,各環均以銅桿與之相接。玩時,依法使九環全部聯貫子銅圈上,或經過穿套全部解下。其解法多樣,可分可合,變化多端。得法者需經過341次上下才能將相連的九個環套入一柱,再用341次才能將九個環全部解下。此外,也可套成花籃、繡球、宮燈等狀。
 巧環
巧環同時,九連環也是按照一種順序來解的。解九連環需要相當一段時間,
這也可以訓練人的耐心。不僅如此,九連環還可以根據需要自行增加環數提高難度,但環數增加將使解開步驟呈幾何級數遞增,且本質上並沒有改變解環方法,因此通常所見仍是九環為主。
西漢才女,辭賦家司馬相如之妻卓文君曾提及九連環:……,七弦琴無心彈,八行書無可傳,九連環從中折斷,十里長亭望眼欲穿;百思想,千懷念,萬般無奈把郎怨。……卓文君生於西漢,諸葛亮生於東漢末年,其時漢室江山已分崩離析。二人相差幾百年。也就是說,在諸葛亮之前幾百年的西漢,九連環已經存在。故“九連環由諸葛亮發明”之說並不正確,可能系後世誤傳。
 巧環
巧環今天,解九連環的世界紀錄是237秒,由中國人王仲彬創造。
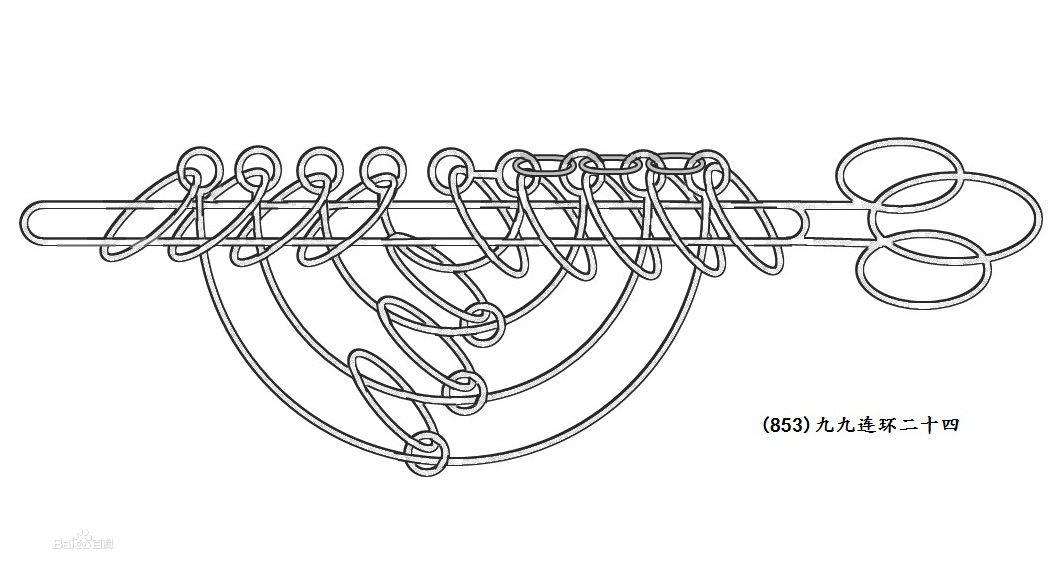 九九連環系列
九九連環系列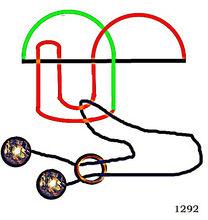 難度比較高的巧繩環圖冊
難度比較高的巧繩環圖冊但是最快的解九連環是1分55秒(115秒),可以在網路上搜尋到視頻。
 實物巧環
實物巧環 巧環
巧環 巧環
巧環 巧環
巧環========================================================================
 巧環
巧環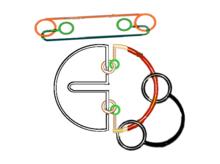 巧環
巧環 巧環穿越與合併2018
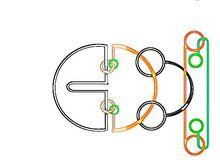
巧環穿越與合併2018探索半開放繩套的解繩巧環
探索半開放繩套的解繩巧環,如圖:
以"1288"新繩環為例,通常巧環初識者會以古老的經過驗證解法的巧環作為嘗試解難環,而對一些新環往往會望而卻步,甚至擔心是否可解等等。
在設計新環過程中發現了一個與拓撲學有關的、有趣的、是否有解判斷方法,對解環玩家應該會有點幫助,陌生的繩環是否有解,如何解開,請看圖示,這裡通常具備兩種條件即為有解,前提是繩套是半開放的。
1、(“假設梁,不假設繩”。)假設虛擬將搭梁的各個關鍵部位分開,就是假設可直接分離,這時如果繩子能解脫,那就是初步可行,第一項驗證通過,但這還不能定論,通常還需要第二項驗證,就是先忽略或直接去掉繩子,之後啟用2。
2、(“假設繩,不假設梁”。)看看這個去掉繩子的環能不能拆成一個沒有結的圓環(原體結構包含無效的扭結除外),如果能就是通過了第二項驗證,此環就是有解的。
但也不排除有罕見特殊的結構還需要第三項驗證(例如獨立纏繞的環樑上另有獨立的圓環等),這需更深的拓撲分析和驗證,不在此淺易論文之中。
對於如圖所示的巧環,僅1、2兩項驗證法足以幫助繩環愛好者解除一些困惑,並可以運用這種方法設計和製作出自己喜愛的、新的"半開放型"解繩巧環。
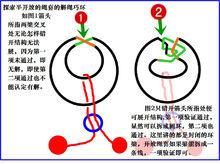
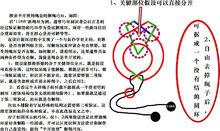
關於1的講解:
 巧環
巧環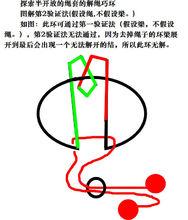 巧環
巧環如圖,箭頭1所指兩梁交叉處無論怎樣錯開結構無法展,因為第一項未通過,即無解,即使第二項通過也不能認定有解。
箭頭2錯開所指處便可展開結構,第一項驗證通過,顯然可以拆成圓環,第二項也通過。這裡講的都是封閉的環梁,開放繩套如果梁能拆成一條線,一項驗證即可。
 巧環
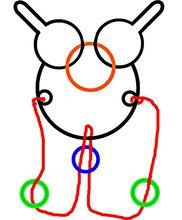
巧環圖解第2驗證法(假設繩,不假設梁。)
如圖:此環可通過第一驗證法(假設梁,不假設繩。),第2驗證法無法通過,因為去掉繩子的環梁展開到最後會出現一個無法解開的結,所以此環無解。
解題測試的科學分析
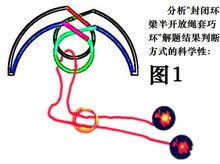
以下分析"封閉環梁半開放繩套巧環"解題結果判斷方式的科學性:(另見<界外驗證法>。
如圖1,以前述兩項測試方式,其結果都能通過,即有解,1圖因為較簡明,容易看出是否存在死結,所以第'一項測試就能判斷結果,那為什麼還要有第二測試呢?因為有些複雜的繞樑環直觀不易看出是否有死結,而死結是不能假設斷梁的,所謂的假設斷梁其實都是繞樑取了捷徑,便於判斷而已,如果在第一測試的假設斷梁時就排除可能存在的死結,即費力又較難準確,所以在第一測試中直接忽略可能的死結,然後再用第二測試檢查是否有死結,這樣比較簡易而且可靠。
或者說,如果在第一測試時能確保死結不參與假設過梁,就無需第二測試了。
那么,這種測試方法科學性如何?是否適用所有同類結構的解繩巧環呢?
圖2是圖1的較複雜化形態,自身的一部分穿過繩與環與另一部分相套繞,按第一測試可以虛擬過梁,過梁後還是圖1的結構,複雜後實際過梁必須過繩套,而環體又不能實際穿環過繩套,但是,此環用前述兩項測試都能通過,即有解,那么它到底有沒有解呢?
本體回套本體並不與本測試衝突,如果這種回套不必須過繩也沒什麼特別,但回套過程必須過繩套,且硬體實體不能穿環,這僅次於出現一個有效參與的死結,上述測試如果通過並且實際可解開,說明該測試理論還是有點科學依據的。
做一個同樣實物直接試試能不能解開,當然可行,即使解開了,但直接解開實物同沒有理論測試基本一樣。
圖3是圖2在不改變原結構的基礎上拓展出來的未解題前的另一狀態,這個狀態顯而易見的證明,前述兩項測試是一種經過驗證而有效的判斷方法。
前面講過,不排除有同類型但非常特殊的加強結構需要第三項測試判斷是否有解的問題。
 巧環
巧環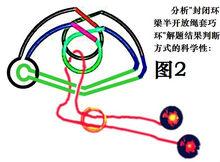 巧環
巧環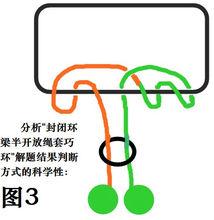 巧環
巧環____________________________________________________________________
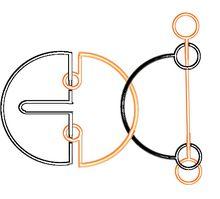
附1、以下是兩款經此驗證法驗證結果的兩款上述類型的新巧環-----(單一封閉的環梁半開放繩套的解繩巧環):
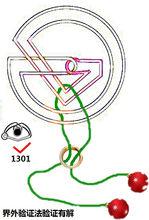 巧環
巧環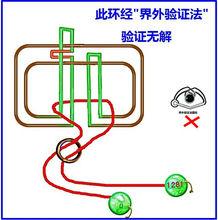 巧環
巧環_____________________________________________________________________________
附2、前文中提到的“不排除有罕見特殊的結構還需要第三項驗證(例如獨立纏繞的環樑上另有獨立的圓環等)”。
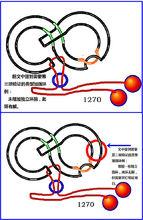 巧環
巧環如下圖:在有解的“1207”上加上一枚獨立圓環後(超出了本測試法現有的允許範圍),它變無解了。
================================================================================
關於巧環釣金鰲結構的分析及套用
 巧環
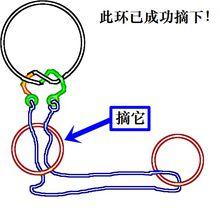
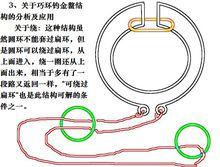
巧環關於巧環釣金鰲結構的分析及套用:
1、如圖,交叉繞樑、無扁環限制,此類結構,去掉繩的梁,只要圓環能夠貫穿過梁就是有解的,但是兩個以上的交叉梁,摘下或裝上圓環後,繩子並不是一下就順利還原,根據壓梁、繞樑的性質和數量不同,解下或裝上圓環後,繩子會自行纏繞出一個或是多個特殊的結,因此還需要單獨”逆向解繩結“將繩子捋順還原即可。理論上只要符合上述條件(無扁環、兩頭獨立不穿套),無論壓繞幾次梁都是有解的。
2、當然,如果帶扁環及兩頭有穿套,那圓環大小起碼要能穿扁環、能套過扁環而且同時能套過兩個頭才可行(如果兩頭不獨立)。
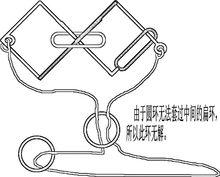 巧環
巧環如下圖, 由於圓環無法套過中間的扁環,所以此環無解。
 3
3
