陳述
 岩澤理論
岩澤理論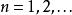 岩澤理論
岩澤理論岩澤健吉起初觀察到代數數論中某些數域所成的 塔的伽羅瓦群同構於p進數所構成的加法群。這個群通常寫作 Γ 並采乘法符號,它是加法群的 逆極限,其中 p是固定的素數而。我們可以用龐特里亞金對偶定理得到另一種表法:Γ 對偶於所有複數域裡的p-次單位根所成的離散群。
歷史
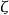 岩澤理論
岩澤理論自岩澤理論在1950年面世起,已經有了一套豐富的理論。人們注意到在模論與黎貝和Heinrich-Wolfgang Leopoldt在1960年定義的p進數L-函式間有根本的聯繫。後者從函式在 負整數點的取值(與伯努利數有關)作插值,得到狄利克雷L函式在p進數域的類比。顯然此理論有希望從庫默爾一個世紀創建前的正則素數理論向前邁進。
“岩澤理論主猜想”被陳述為:以兩種不同方法定義的 p進數L-函式(模理論/插值法)應當相等,只要它們是明確定義的。這個猜想在Q上的情形最後由貝利·馬祖爾(Barry Mazur)與安德魯·懷爾斯證明,並由懷爾斯證明所有實域的情形,稱作馬祖爾-懷爾斯定理。他們仿造肯尼斯·阿蘭·黎貝證明埃爾布朗定理之逆定理(即所謂埃爾布朗-黎貝定理)的辦法。
近來 Chris Skinner 與 Eric Urban 也仿用肯尼斯·阿蘭·黎貝的辦法,公布了GL(2) 的“主猜想”的一個證明。藉由 Kolyvagin 發展的歐拉系統,可以得到馬祖爾-懷爾斯定理更初等的證明(請參見 Washington 的書)。 Karl Rubin 等人用歐拉系統得到主猜想其它的推廣形式。
例子
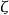 岩澤理論
岩澤理論設為p次本原根,並考慮下述數域所成的塔:
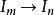 岩澤理論
岩澤理論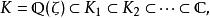 岩澤理論
岩澤理論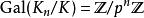 岩澤理論
岩澤理論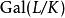 岩澤理論
岩澤理論其中K是p 次本原根生成的數域。這個塔的聯集稱作L。由於,同構於 Γ 。為了得到一個有趣的伽羅瓦模,岩澤健吉取K的理想類群,並令I為其p-撓部分。對於m>n,有 範數映射,於是得到一個逆系。令 I 為其逆極限, Γ 作用其上,我們欲描述這個作用。
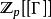 岩澤理論
岩澤理論毫無疑問,這裡的動機在於 K 的理想類群的p-撓部分已被恩斯特·庫默爾認出是他證明費馬大定理的主要障礙。岩澤健吉的創見在於他在一個新的意義上“跑到無窮大”。事實上,I是群環的完備化上的模;這個環性質很好(它是一個二維正則局部環),這意味著我們可以對其上的模作夠精細的分類。
