基本概念
小腦模型關節控制器（CMAC）是由含局部調整，相互覆蓋接受域的神經元組成，J.S.Albus於20世紀70年代提出了CMAC，它是模擬人的小腦的一種學習結構，是基於表格查詢式輸入輸出的局部神經網路模型，提供了一種從輸入到輸出的多維非線性映射能力。由於CMAC具有學習速度快、泛化能力強、易於實現、不存在局部極小點等特點，被廣泛地套用於對實現性要求較高的控制系統中，作為辯識器和控制器，並取得了較好的效果。
小腦模型關節控制器
結構
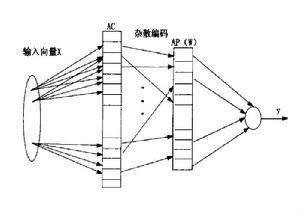
其結構見圖1所示，由兩個基本映射表示輸入輸出之間的非線性關係。
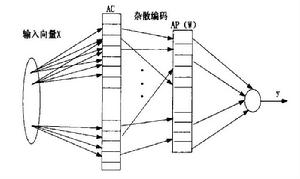小腦模型關節控制器網路圖1
（1）概念映射（X→ AC）
設n維輸入向量為X，經量化編碼後，映射至AC中c個存儲單元中，在輸入空間鄰近的兩個點，AC中有部分的重疊單元被激勵。距離越近，重疊越多；距離遠的點，AC中不重疊，即相近的輸入產生相近的輸出。
（2）實際映射（AC→AP）
實際映射是由概念存儲器AC的c個單元映射至實際存儲器AP的c個單元，這c個單元中存放著相應的權值，則網路的輸出為AP中c個單元的權值之和。
在CMAC中，若輸入維數較高，則AC要有很大的容量。但對於特定的問題，在AC中被激勵的非零單元是很稀疏的，用雜散存儲，可將AC空間壓縮到較小的AP中。
算法
傳統的CMAC網路權值的調整一般採用Widrow-Hoff規則，即LMS方法，如下式：
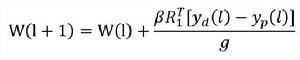小腦模型關節控制器網路
小腦模型關節控制器網路其中，g是泛化常數， 是學習率。
這種算法實現容易、學習速度快，但它是用分段超平面去擬和非線性超曲面，因此，不能學習所逼近的導數，並且精度不高。很多學者對CMAC的學習算法進行改進，進而達到提高網路收斂速度和精度的目的。其中最具代表性的是Chang-TsanChinang和Hun-ShinLin於1996年提出在輸出層引入了廣義基函式（GBF）取代了原有網路輸出層上的線形映射。可以說是CMAC研究的一大突破。它的優越之處在於當基函式採用可微函式時，可記憶系統的微分信息，而傳統的CMAC可看作是基函式為1的網路。當然，其代價是增大了計算量，並且收斂速度比傳統CMAC網路大大降低。其連線權的學習算法為：
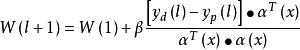小腦模型關節控制器網路其輸出為：
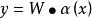小腦模型關節控制器網路
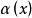小腦模型關節控制器網路其中： 為基函式，可用B樣條插值函式等。
為了克服廣義基函式CMAC的缺陷，很多學者在此基礎上又做了進一步的改進，如段培勇等在此基礎上提出了改進的基於廣義基函式的CMAC學習算法，使收斂條件不依賴於基函式和樣本數據，且學習速度快。
從某種意義上來說，CMAC與模糊邏輯不但是相互補充的，而且也是相通的、可以結合的。首先，利用連線主義表達的模糊邏輯控制器必然要引入學習機制，也帶來了兩者結合的諸多優點，如存儲容量的減小，泛化能力的提高以及連線主義結構的容錯性等。其次，CMAC的分布表達式中，一個值由散布於許多計算單元的活性模式表示，每個計算單元有涉及許多不同值的表達，因此每個計算單元都有一個感受野，即它所表達的所有值的集合，這相當於每個計算單元都對應一個模糊集合，或者說感受野相當於隸屬函式。這正是它們能夠相結合的一個基礎。因此，基於模糊的CMAC也不斷地被廣大學者所關注，有著很好的套用前景。
收斂性分析
1992年，Wong對CMAC的收斂性進行了分析，得出了當採用增量學習法，學習率為1時，CMAC算法CMAC算法本身保證了它的收斂性的結論，當輸入是多維時，上述結論不一定成立。其他人在Wong的基礎上，對CMAC的收斂性進行了進一步研究但其結論是在關聯矩陣正定的特殊條件下得到的。何超等在Wong提出的算法表達形式出發，分析了CMAC增量算法在批量和增量兩種學習方式下的收斂性，給出這種算法的一般性定理：
定理1
小腦模型關節控制器網路CMAC批量學習算法的充要條件是學習率 滿足
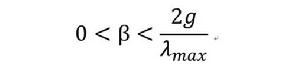小腦模型關節控制器網路其中，λmax>0是關聯矩陣C的最大特徵值。
定理2
小腦模型關節控制器網路 小腦模型關節控制器網路CMAC增量學習算法的必要條件是學習率 滿足0< <2。特別地，當CMAC輸入向量是1維量，成為增量學習算法的充要條件。
這兩個收斂性分析的定理為CMAC的套用提供了理認依據，但對於CMAC其它算法收斂性的證明，仍須進一步的研究。
CMAC神經網路
CMAC神經網路建模
CMAC作為萬能逼近器，可用來建立系統的輸入輸出模型。狀態空間表達式可以完全描述線形系統的全部動態行為。除此之外，對於線形系統，傳遞函式矩陣提供了定常係數的黑箱式輸入輸出。在時域中，利用自回歸滑動平均模型（ARMA），通過各種參數估計方法，也可以給出系統的輸入輸出描述。但對於非線性系統，基於非線性自回歸滑動平均模型（NARMA），卻難以找到一個恰當的參數估計方法，傳統的非線性控制系統辯識方法，在理論研究和實際套用中都存在極大的困難。
相比之下，神經網路在這方面顯示出明顯的優越性。由於神經網路具有通過學習逼近任意非線性映射的能力，將神經網路用於非線性系統的建模與辯識，可以不受非線性模型的限制，而且便於給出工程上易於實現的學習算法。套用表明，CMAC的學習快速性特別適合於線上建模與校正。
CMAC神經網路控制
基於CMAC的控制方案有多種，主要有：
（1）神經網路直接逆控制。將被控對象的神經網路逆模型直接與被控對象串聯起來，以便使期望輸出與對象實際輸出之間的傳遞函式等於1，從而在將此網路作為前饋控制器後，使被控對象的輸出為期望輸出。
（2）神經網路模型參考自適應控制神經網路控制器的作用是使被控對象與參考模型輸出之差的二次型最小。
（3）神經網路自校正控制。根據對系統正向或逆模型辯識的結果，直接調節控制器內部參數，是系統滿足給定的性能指標。
（4）神經網路內模控制。在內模控制中，系統的正向模型與實際系統並聯，兩者輸出之差被用作反饋信號，此反饋信號又由前向通道的濾波器及控制器進行處理。該控制器直接與系統的逆有關，而引入濾波器的作用是為了獲得期望的魯棒性和跟蹤回響。
（5）用CMAC進行非線性系統線形化。
CMAC神經網路與其他控制策略相結合，相互取長補短，得到更好的控制效果。如：
（1）模糊CMAC（FCMAC）控制。利用神經網路的自組織和競爭學習功能，獲得模糊邏輯規則，使CMAC與模糊邏輯的優勢結合起來，具有較好的控制效果。
（2）神經網路專家系統控制。專家體統善於表達知識和邏輯推理，將二者結合，發揮各自的優勢，就會獲得更好的控制效果。
（3）用遺傳算法進行神經網路的結構及參數的最佳化。
（4）神經網路預測控制通過離線學習實際系統的輸入輸出數據，CMAC可逼近系統的動態性能，在控制時，CMAC可作為輸出預測器，用以預測未來輸出，從而實現預測控制。
CMAC的優越性
神經網路可分為全局逼近神經網路和局部逼近神經網路，如果網路的一個和多個連線權係數或自適應可調參數，在輸入空間的每一點對任何一個輸出都有影響，則稱該神經網路為全局逼近網路。如BP網路，每一次樣本學習都需要重新調整網路的所有權值，收斂速度慢，易陷入局部最小，很難滿足控制系統的實時性要求;若對輸入空間的某個局部區域，只有少數幾個連線權影響網路的輸出，則稱該網路為局部逼近網路，從而使局部逼近網路具有學習速度快的優點。CMAC、RBF以及某些模糊神經網路是局部逼近網路。
CMAC比其他神經網路的優越性體現在：
（1）CMAC神經網路把信息存儲在局部的結構上，在保證函式逼近的前提下，學習速度快。
（2）CMAC函式逼近器對學習數據出現的次序不敏感，因此，CMAC在時變、非線性系統控制中得到廣泛套用。
（3）CMAC結構簡單，易於硬體實現和軟體實現。
因此，CMAC已被越來越多的學者所關注，並得到廣泛的套用。
CMAC的套用及發展
套用
目前，CMAC已被有效地套用於非線性函式的逼近、非線性系統的反饋線性化、動態建模、控制系統的設計等，如機器人的控制、精餾塔控制、壓電刀架控制、車輛智慧型報警系統、信號處理、燃料供給系統控制、印表機色彩校準、高精度泵控馬達位置伺服系統的控制、液壓電梯實時控制系統、非線性預測控制、Wiener模型的辯識等中，並取得了較好的控制效果。
由於CMAC具有學習速度快、泛化能力強、易於實現、不存在局部極小點等特點，被廣泛地套用於對實現性要求較高的控制系統中，作為辯識器和控制器，並取得了較好的效果。
需要解決的問題
CMAC神經控制的目標是在降低計算量的情況下，尋找快速全局收斂的學習算法，以及其於CMAC尋找具有很強魯棒性的全局穩定的控制策略，並且在實際套用中易於實現。鑒於目前CMAC神經控制的現狀，有以下幾個方面的問題需要解決。
（1）高維輸入記憶單元的劇增問題。很多學者曾做了很多工作，但缺乏理論依據。
（2）控制系統魯棒性。目前，神經控制的研究側重於沒有干擾或神經網路預測器沒有誤差時的學習算法的收斂性與控制系統的穩定性，而忽略了魯棒性。實際上，神經控制的魯棒性是非常重要的，特別是用在過程控制中。同時，魯棒性也是神經控制的弱點。
（3）快速有效學習算法的研究。
（4）CMAC輸入維數、泛化常數及學習率的確定。這些參數的合理確定，對系統的性能有著重要的影響。
（5）廣義基函式的選取。
（6）神經控制系統的能控性、能觀性及穩定性判定。
近年來，對CMAC本身的研究，如網型等未再有根本的突破，專門適用於控制問題的動態CMAC仍有待於進一步發展。儘管如此，目前對神經網路及其控制方法的研究仍然方興未艾。將模糊邏輯、專家系統和機器學習等方法融合於CMAC控制，發展具有不同智慧型粒度的綜合集成系統，仍極具發展潛力，可以說代表了CMAC極其控制方法的主要發展趨勢。
