基本介紹
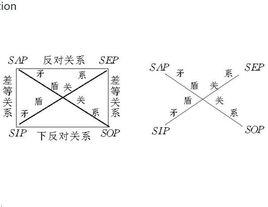
對當關係是A,E,I,O四種主謂詞相同的直言命題之間的真假關係的統稱。A,E,I,O分別為全稱肯定、全稱否定、特稱肯定、特稱否定命題的記號。A與O,E與I之間不能同真,又不能同假,稱為矛盾關係;A與E不能同真,可以同假,稱為反對關係;A真時,I也真,但反之不然;I假時,A也假,但反之不然,稱為差等關係(E與O之間也是差等關係)。I與O不能同假,可以同真,稱為下反對關係。傳統邏輯預設S,P都不是空集,故有上述對當關係。上述四種關係可用如圖1的邏輯方陣表示,如果S,P是空集,則對當關係中只有矛盾關係成立,此時,應改為如圖2的邏輯方陣 。
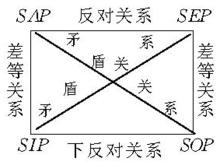 圖1
圖1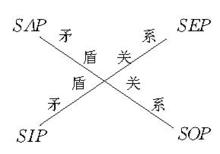 圖2
圖2對當關係推理
概念
對當關係推理:對當關係推理是指依據邏輯方陣,在同一素材的A,E,I,O四種性質判斷之間進行的推理 。
對當關係推理的分類
a.從屬關係推理(差等關係推理) ;
Ⅰ.從全稱判斷的真推出特稱判斷真:
SAP真→SIP真
SEP真→SOP真
例如:
①從“所有事物是運動變化的”真,推出“有的事物是運動變化的”真。
②從“所有謊言都不是能長久欺騙人的”真,推出“有的謊言不能長久欺騙人”真。
Ⅱ.從特稱判斷假推出全稱判斷假:
SIP假→SAP假
SOP假→SEP假
例如:
①從“有些物體是不動的”假,推出“所有物體是不動的”假。
②從“有些疾病不傳染”假,推出“所有疾病不傳染”假。
b.反對關係推理:
Ⅰ.上反對關係:從一個判斷真,推出另一個判斷的假。
SAP真→SEP假
SEP真→SAP假
例如:
①從“所有公民都要守法”真,推出“所有公民都不要守法”假:
②從“所有的樣品都不出售”真,推出“所有的樣品都出售”假:
Ⅱ.下反對關係:從一個判斷假,推出另一個判斷真。
SIP假→SOP真
SOP假→SIP真
例如:
①從“有的天鵝是黑的”假,推出“有的天鵝不是黑的”真。
②從“有的人不是自私的”假,可推知“有的人是自私的”真。
c.矛盾關係推理:
Ⅰ.從一個判斷真推出另一個判斷假。
SAP真→SOP假
SEP真→SIP假
SIP真→SEP假
SOP真→SAP假
例如:
①從“所有中國人都是炎黃子孫”真,推出“有的中國人不是炎黃子孫”假。
②從“所有侵略戰爭都不是正義戰爭”真,推出:“有的侵略戰爭是正義戰爭”假。
③從“有的黨員是知識分子”真,推出“所有黨員不是知識分子”假。
④從“有的人不是南方人”真,可推知“所有人是南方人”假。
Ⅱ.從一個判斷的假推知另一個判斷真。
SAP假→SOP真
SEP假→SIP真
SIP假→SEP真
SOP假→SAP真
例如:
①從“所有人都是自私的”假,可推知“有的人不是自私的”真。
②從“所有人都不是自私的”假,可推知“有的人是自私的”真。
③從”有的樣品出售”假,可推知“所有樣品都不是出售的”真。
④從“有的工藝品不是出售的”假,可推知“所有工藝品是出售的”真 。
| 推理根據 | 推理形式 |
| 反對關係 | SAP→並非SEP SEP→並非SAP |
| 下反對關係 | 並非SIP→SOP 並非SOP→SIP |
| 差等關係 | SAP→SIP SEP→SOP 並非SIP→並非SAP 並非SOP→並非SEP |
| 矛盾關係 | SAP←→並非SOP SEP←→並非SIP SIP←→並非SEP SOP←→並非SAP |