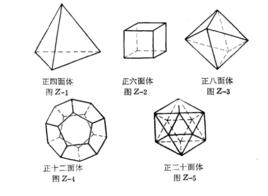
基本介紹
正多面體是凸多面體,其各面皆系全等正多邊形,且所有多面角均相等,正多面體中每一個頂點通過的棱數是相同的。
歐幾里德證明,僅存在有五種正多面體:正四面體(圖1)、正六面休或正方體(圖2)、正八面體(圖3)、正十二面體(圖4)和正二十面體(圖5)。每一種正多面體都可以利用平面截割正方體的方法得到。所有正多面體,除了正四面體而外,都有對稱中心,所有正多面體都有一個外接球和一個內切球,正四面體與其本身是對偶的;正方體與正八面體是對偶的;正十二面體和正二十面體是對偶的。正多面體的頂點個數等於和它對偶的正多面體的面數。兩對偶正多面體的棱數相同,正多面體各面的中心是其對偶正多面體的頂點 。
 對偶正多面體
對偶正多面體 對偶正多面體
對偶正多面體對於正多面體,且對於零類多面體,歐拉定理成立:,其中B——頂點數,——面數,p——多面體的棱數。
 正四面體 正四面體 |  正六面體 正六面體 | 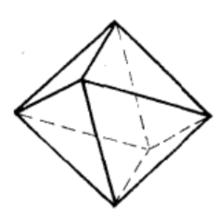 正八面體 正八面體 |
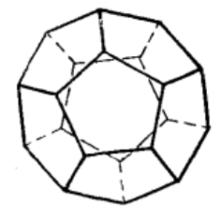 正十二面體 正十二面體 | 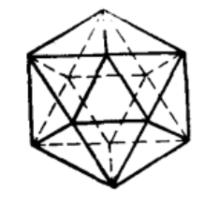 正二十面體 正二十面體 |
| 面的種類 | 頂點個數 | 棱個數 | 圍繞一個頂點的面的個數 | 面個數 | |
| 正四面體 | 正三角形 | 4 | 6 | 3 | 4 |
| 正六面體 | 正四邊形 | 8 | 12 | 3 | 6 |
| 正八面體 | 正三角形 | 6 | 12 | 4 | 8 |
| 正十二面體 | 正五邊形 | 20 | 30 | 3 | 12 |
| 正二十面體 | 正三角形 | 12 | 30 | 5 | 20 |
相關問題
1.我們考察凸多面體,它的頂點是某個正多面體的界面的中心,證明:這個多面體也是正多面體。(它叫做原來多面體的對偶多面體)。
提示 當關於原來的多面體的頂點同它的中心連線的直線旋轉時,多面體變作自身,與這個頂點毗鄰的界面的中心變作自身,也就是,它們是正多面體的頂點,類似地,考察關於連線原來的多面體界面的中心同它的中心的直線的旋轉,我們得到對偶多面體的多面角是正的,因為運動能使原來多面體的任意兩個多面角重合,對偶多面體的所有界面相等,又因為原來多面體的任兩個界面能夠重合,對偶多面體的所有多面角相等 。
2.a)證明:四面體的對偶多面體是四面體。
b)證明:立方體與八面體彼此對偶。
c)證明:十二面體與二十面體彼此對偶。
提示 為了證明只需注意,如果原來多面體在頂點的是m個界面的角和n邊形界面,那么,它的對偶多面體的頂點是n個界面的角和m邊形界面。
3.證明:如果兩個彼此對偶的正多面體的內切球的半徑相等,那么 :
a)它們的外接球的半徑相等;b)它們界面的外接圓半徑相等。
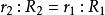 對偶正多面體
對偶正多面體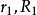 對偶正多面體
對偶正多面體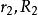 對偶正多面體
對偶正多面體提示 a)設O是原來多面體的中心,A是它的一個頂點,B是帶有頂點A的一個界面的中心。我們考察原來的多面體毗鄰頂點A的界面的中心。設C是這個界面的中心,即,這個界面與直線OA的交點,顯然,AB⊥OB和BC⊥ OA,所以OC:OB=OB:OA,即,其中(相應的)是原來多面體的(對應的它的對偶多面體的)內切球和外接球的半徑。
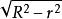 對偶正多面體
對偶正多面體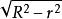 對偶正多面體
對偶正多面體b)如果由半徑為R的球面的中心到平面的距離為r,那么球面被平面截出的圓的半徑等於,所以在半徑為R的球中內接的和在半徑為r的球面外切的多面體的界面的外接圓的半徑,等於。特別地,如果兩個多面體的R和r相等,那么它們相等且它們界面的外接圓半徑相等。
4. 十二面體的一個界面和二十面體的一個界面在一個平面上,此外,它們的相對的界面也在一個平面上,證明:剩下的十二面體和二十面體的所有頂點位於在平行於這些界面的兩個平面上。
提示 如果十二面體和二十面體外切在一個球面上,那么它們的外接球的半徑相等(問題3a)),也就是它們相對界面之間的距離相等,我們將十二面體(或二十面體)的外接球面與通過它的中心和一個界面中心的直線的交點,稱為“球界面的中心”,我們確定十二面體的一個球界面中心並考察它到各頂點的距離;這些距離中恰有四個不同的,為了解決問題只需證明,這四個不同距離的組成同對二十面體的這個組成是重合的就夠了。
容易檢驗,十二面體的球界面中心是二十面體的頂點,而得到的二十面體的球界面中心是原來十二面體的頂點。所以球界面中心和十二面體頂點之間的任何距離是二十面體的球界面中心和頂點之間的距離 。