基本介紹
在最小二乘估計技術族中，既有單一方程估計法，像直接與間接的最小二乘法、二階段最小二乘法和最小方差比估計法，又有系統估計法，即利用整個系統經濟模型的結構性質並同時對所有的結構參數進行估計的方法，如三階段最小二乘法。類似地，在最大似然估計技術族中，有單一方程估計法(如有限信息最大似然法)，也會有系統估計法。這種系統估計法被人們稱為 完全信息 最大似然法(Full Information Maximum Likelihood Estimator，簡稱FIML) 。
完全信息最大似然法指在同時考慮所有結構方程的約束的前提下，用最大似然法估計結構方程的參數。完全信息最大似然法是一種系統估計方法，它適用於過度識別的方程系統。這種方法是先求擾動項的似然函式，然後根據關於擾動項的似然函式導出關於內生變數的似然函式。最後求似然函式在所有約束條件下的極大似然值 。
FIML法的假設
1. FIML法要求使用完全信息，即要求對整個模型是完全了解的，不但需要知道在模型中出現的所有內生變數和所有前定變數，而且需要知道每個方程式的數學形式。這就必須正確設定所有結構方程式。
2. 要求每個結構方程式都是可識別的(恆等式除外)，特別允許是過度識別的。如果模型中有某些結構方程式不能識別，那么該模型必須重新設定。
3. 每個結構方程式的隨機擾動項要求滿足通常的假定：零平均值，同方差，序列無關，遵從常態分配 。
FIML法和LIML法的比較
FIML法和LIML法的比較：
相同點：
(1)它們都是從ML法發展改進而來的。
(2)它們都適合於過度識別的結構方程式。
(3)它們所求得的參數的估計量都具有一致性特性。
相異點：
(1)LIML法是單一方程方法，FIML是方程組方法。
(2)LIML法只使用了“有限信息”，而FIML法使用了“完全信息”，在這種意義上，FIML法比LIML法更為有效。
(3)FIML法比LIML法計算過程複雜，要花費更多的時間和付出更多的成本。
關於FIML的幾點說明
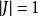完全信息最大似然法1. 當方程組模型是遞歸式時，由於雅可比行列式，那么完全信息極大似然估計量所滿足的方程組對估計量是線性的。在這樣的情況下較易於求解。
2. FIML法要求對整個聯立方程組模型都要正確設定。與其它方法相比較對設定誤差更為敏感。
3. 由於要同時求出模型中所有參數的估計量，因此要求樣本容量足夠大。又由於在求解估計量時，涉及關於參數的非線性方程組，這是較為困難的工作。因此，FIML法在實際工作中還沒有被普遍使用 。
