婆羅摩笈多
婆羅摩笈多在算術方面的工作與阿耶波多第一不相上下。在幾何方面有作圖問題，如已知三角形兩邊及第三邊上的高作三角形、作等腰梯形、作三邊相等的梯形等。在幾何計算問題上有求內接於圓的四邊形的面積和對角線的公式,若四邊形的邊長分別是α、b、с、d，則它的面積是
，
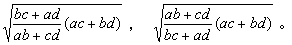
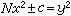的二次不定方程都是婆羅摩笈多的創見。 參考書目
S.Prakash,A Critical Study of BrahMagupta and His Wor噚,The Indian Institute of Astronomical and Sanskrit Research, New Delhi,1968.
A.K.Bag,Mathematics in Ancient and Medieval India,New Delhi, 1979.
主編著作
婆羅摩笈多在30歲左右，編著了《婆羅摩修正體系》(Br1hma-sphuatasiddh1nta，公元628年)一書．該書用此名，是因為他修改和引用了印度最古老的天文學著作《婆羅摩體系》(Brāhmasiddh1nta)的內容．《婆羅摩修正體系》分為24章，其中《算術講義》(Ganit1d’h1ya)和《不定方程講義》(Kutakh1dyaka)兩章是專論數學的，前者研究三角形、四邊形、零和負數的算術運算規則、二次方程等；後者研究一階和二階不定方程．《婆羅摩修正體系》的其他各章是關於天文學研究的，也涉及到許多數學知識．婆羅摩笈多的另一部著作《肯達克迪迦》(Khandakh1dyaka，音譯)，是天文學方面的名著．它包含8章，研究了行星的黃經，與周日運動有關的三個問題，月食、日食、星的偕日升落，以及行星的會合等．婆羅摩笈多的這些著作在拉賈斯坦邦、古吉拉特邦、中央邦、北方邦、比哈爾、尼泊爾、潘賈婆(Panjab)和克什米爾等地受到廣泛重視，許多學者對其進行過研究．
婆羅摩笈多的一些數學成就在世界數學史上有較高的地位，他提出了負數概念，用小點或小圈記在數字上面以表示負數，並給出負數的運算法則，如“兩個正數之和為正數，兩個負數之和為負數，一個正數和一個負數之和等於它們的差”；“一個正數與一個負數的乘積為負數，兩個負數的乘積為正數，兩個正數的乘積為正數”等等．他的負數概念及其加減法法則，僅晚於中國(約公元1世紀成書的中國《九章算術》最早提出負數及其加減法運算的概念)而早於世界其他各國數學界；而他的負數乘除法法則，在全世界都是領先的．
突出貢獻
婆羅摩笈多對數學的最突出貢獻是解不定方程Nx2+1=y2．在歐洲，這類方程由費馬提出，但後來歐拉誤記為佩爾提出，並寫入他的著作中。後人多稱佩爾方程。沿續至今。1767年，J．L拉格朗日(Lagrange)運用連分數理論，給出了該問題的完全的解答．事實上，婆羅摩笈多在公元628年便幾乎完全解出了這種方程，只是當時不為歐洲人所知．其後，婆羅摩笈多的解法又被婆什迦羅(Bh1skara)改進．[1]