方程式
外爾方程式的廣義形式可寫為:
 外爾方程
外爾方程在SI單位中可寫為:
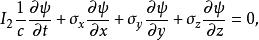 外爾方程
外爾方程其中
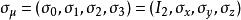 外爾方程
外爾方程為一向量。μ = 0分量為2 × 2單位矩陣;μ = 1,2,3分量為泡利矩陣。ψ則是波函式,為外爾旋量一例。
外爾旋量
其組成有ψ與ψ,分別為左手(Left-handed)外爾旋量及右手(Right-handed)外爾旋量,各自有兩個分量。兩者皆有下列形式:
 外爾方程
外爾方程其中
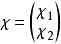 外爾方程
外爾方程為具有二常數分量之旋量。
既然粒子是不具質量的,亦即 m= 0,動量 p的範數為波向量 k的簡單乘積,由德布羅伊關係所描述:
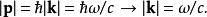 外爾方程
外爾方程方程式可以左手及右手旋量來表示:
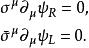 外爾方程
外爾方程推演
透過拉格朗日密度可得方程式:
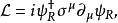 外爾方程
外爾方程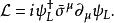 外爾方程
外爾方程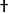 外爾方程
外爾方程將旋量及旋量的埃爾米特伴隨(以標記)當作獨立變數處理,則可得外爾方程式。
相關條目
•狄拉克方程式(描述帶質量的自旋½粒子)
•角動量算符
•動量算符
•自旋
