定義
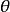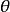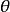基佩特雙曲線
基佩特雙曲線 基佩特雙曲線 基佩特雙曲線
基佩特雙曲線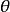 基佩特雙曲線 基佩特雙曲線 基佩特雙曲線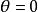
基佩特雙曲線
基佩特雙曲線
基佩特雙曲線平面上一三角形ABC，由三邊BC CA AB為底邊，做底角為 的等腰三角形，規定 >0時向外， <0時向內作。設得到的三個三角形分別為 ABD CAE BCF ，連AF BE CD 則這三條直線交於一點，設為G。當 在 中變動時（ 時定義G為三角形的重心， 時定義G為三角形的垂心），G點的軌跡為一條雙曲線，稱為三角形ABC的基佩特雙曲線。
性質
1：任意三角形的基佩特雙曲線都經過三角形三頂點
2：任意三角形的基佩特雙曲線都是等軸雙曲線
3：任意三角形的基佩特雙曲線都過三角形的重心，垂心，費爾馬點
4：基佩特雙曲線的中心在九點圓上
