計算方法
地下水在孔隙或裂隙中的運動稱為滲流。它在一定條件下符合線性滲流定律(即達西定律)。
v=kJ (1)
式中，v為地下水滲流速度；k為滲透係數；J為水力坡降(即單位距離的水位差)。
在多孔介質中的地下水流，當雷諾數大於10時，其水流狀態為非線性層流。水流隨著雷諾數的增大而逐漸過渡到紊流狀態區，運動不再符合達西定律。在紊流運動條件下，地下水的滲流服從謝才公式。
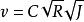地下水鹽運動(2)
式中，C為謝才係數；R為水力半徑。
在自然條件(降雨、蒸發等)和人為因素(如灌溉、排水和修建水工建築物等)影響下，地下水形成水力坡降而產生運動。
地下水含水層中鹽分運動即溶質運移，主要通過擴散(水動力彌散)和對流2種途徑。由於溶質的分子擴散和彌散作用，可用菲克定律表示，即通過單位斷面面積的溶質通量與溶質濃度的梯度成正比。在均質各向同性條件下，可寫成如下關係式：
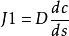地下水鹽運動(3)
式中，J1為由於水動力彌散作用而產生的溶質通量；dc/ds為溶質濃度梯度；D為彌散係數。
由於對流而產生的溶質通量，即隨同地下水運動而產生的溶質通量為
J2=μ0vc (4)
式中，J2為由於對流作用而產生的溶質通量；為含水層的有效孔隙率；D為地下水的孔隙平均流速；C為溶質在地下水中的濃度。
地下水中的鹽分是隨水流而運移的，水動力彌散和對流2種作用往往同時存在，但在某些情況下可能以某一作用為主，而另一種作用則處於次要地位。在已知地下水流各項要素和水鹽運動基本參數的情況下，可通過式(3)、式(4)求得鹽分的運移通量。
