定義
因果系統,即輸入的回響不可能在此輸入到達的時刻之前出現的系統;也就是說系統的輸出僅與當前與過去的輸入有關,而與將來的輸入無關的系統。
系統的這種特性稱為因果特性。符合因果性的系統稱為因果系統或非超前系統 (nonanticipative system)。與之相對的有非因果系統和反因果系統。
非因果系統(noncausal system)是輸出不僅與當前的輸入,而且與將來的輸入有關的系統。
反因果系統(anticausal system)是輸出僅與將來的輸入有關的系統。
因果性的判斷
對於連續時間系統:
t=t1的輸出y(t1)只取決於t≤t1的輸入x(t≤t1)時,則此系統為因果系統,
特殊的:當該系統為線性移不變系統時,系統的衝激回響函式h(t),在t<0的條件下,h(t)=0,則此系統為因果系統;如果系統的單位衝激回響在t>0時,h(t)=0,就說該系統是反因果的。
對於離散時間系統:
n=n1的輸出y(n1)只取決於n≤n1的輸入x(n≤n1)時,則此系統為因果系統,
特殊的:當該系統為線性時不變系統時,系統的衝激回響函式h(n),在n<0的條件下,h(n)=0,則此系統具有因果性,為因果系統。
因果系統的意義
因果系統固然重要,但並不是所有有實際意義的系統都是因果系統。
1. 在圖像處理中,變數不是時間,此時,因果往往不是根本性的限制。
2. 非實時情況,待處理的數據實現記錄下來,例如為了去除噪聲的變化,保留總體的緩慢變化趨勢,常作取平均:
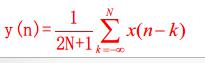 圖1 公式
圖1 公式因果系統的系統表達式
LSI系統是因果系統的充分必要條件,即系統表達式要滿足:
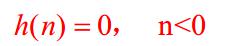 圖2 公式
圖2 公式對一個線性系統,它的因果性就等效於初始鬆弛條件。
將n<0,x(n)=0的序列叫因果序列,表示這個因果序列可以作為一個因果
系統的單位抽樣回響。
判定 LTI 系統的因果性
對於給定的常係數 N 階差分方程:
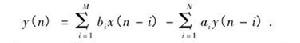 圖3 公式
圖3 公式若根據初始條件, 假定經過判定描述的是一個 LTI 系統, 則必有如下結論:
如果初始條件為 y(n) =0, n <0 或 y( -1)、 y( -2)、 …、y( - N)皆為零, 即系統無初始儲能, 處於零狀態, 則系統必為因果的。反之, 如果 y( - 1)、 y( - 2)、 …、 y( - N)不全為零, 則系統必為非因果的。
證明如下:
若系統為 LTI 系統, 則因果性判定如下:
因為 h(n) = y(n)
x(n) = δ(n) ,
若初始條件 y(n) =0, n <0 .
則 h(n) = y(n)
x(n) = δ(n) =0, n <0 .
由此可知系統為因果系統, 反之,y(n) =0, n <0 不
成立, 如 y( -2) =1, 則
h( -2) = y( -2)
x(n) = δ(n) =1, n <0 .
此時可知, 系統為非因果系統, 證畢。
上述結論換句話說就是:對於差分方程描述的 LTI 系統, 如果初始條件為 0 則為因果系統, 反之為非因果系統
