試驗設計
試驗設計與最佳化方法,都未能給出直觀的圖形,因而也不能憑直覺觀察其最最佳化點,雖然能找出最優值,但難以直觀地判別最佳化區域.為此回響面分析法(也稱回響曲面法)應運而生.回響面分析也是一種最最佳化方法,它是將體系的回響(如萃取化學中的萃取率)作為一個或多個因素(如萃取劑濃度、酸度等)的函式,運用圖形技術將這種函式關係顯示出來,以供我們憑藉直覺的觀察來選擇試驗設計中的最最佳化條件.
 回響面
回響面顯然,要構造這樣的回響面並進行分析以確定最優條件或尋找最優區域,首先必須通過大量的量測試驗數據建立一個合適的數學模型(建模),然後再用此數學模型作圖.
建模最常用和最有效的方法之一就是多元線性回歸方法.對於非線性體系可作適當處理化為線性形式.設有m個因素影響指標取值,通過次量測試驗,得到n組試驗數據.假設指標與因素之間的關係可用線性模型表示,則有套用均勻設計一節中的方法將上式寫成矩陣式或簡記為式中表示第次試驗中第個因素的水平值;為建立模型時待估計的第個參數;為第次試驗的量測回響(指標)值;為第次量測時的誤差.套用最小二乘法即可求出模型參數矩陣B如下將B陣代入原假設的回歸方程,就可得到回響關於各因素水平的數學模型,進而可以圖形方式繪出回響與因素的關係圖.
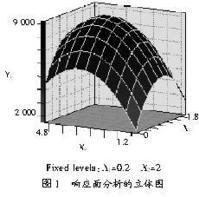
模型中如果只有一個因素(或自變數),回響(曲)面是二維空間中的一條曲線;當有二個因素時,回響面是三維空間中的曲面.下面簡要討論二因素回響面分析的大致過程.
在化學量測實踐中,一般不考慮三因素及三因素以上間的互動作用,有理由設二因素回響(曲)面的數學模型為二次多項式模型,可表示如下:通過n次量測試驗(試驗次數應大於參數個數,一般認為至少應是它的3倍),以最小二乘法估計模型各參數,從而建立模型;求出模型後,以兩因素水平為X坐標和y坐標,以相應的由上式計算的回響為Z坐標作出三維空間的曲面(這就是2因素回響曲面).
應當指出,上述求出的模型只是最小二乘解,不一定與實際體系相符,也即,計算值與試驗值之間的差異不一定符合要求.因此,求出係數的最小二乘估計後,應進行檢驗.一個簡單實用的方法就是以回響的計算值與試驗值之間的相關係數是否接近於1或觀察其相關圖是否所有的點都基本接近直線進行判別.如果以表示回響試驗值,為計算值,則兩者的相關係數R定義為其中對於二因素以上的試驗,要在三維以上的抽象空間才能表示,一般先進行主成分分析進行降維後,再在三維或二維空間中加以描述.等等…………
注意事項
對於構造高階回響面,主要有以下兩個問題:
1, 抽樣數量將顯著增加,此外,普通的實驗設計也將更糟。
2,高階回響面容易產生振動。
回響面說明什麼?
回響面法(response surface methodology,記為RSM)最早是由數學家Box和Wilson於1951年提出來的。就是通過一系列確定性的“試驗”擬合一個回響面來模擬真實極限狀態曲面。其基本思想是假設一個包括一些未知參量的極限狀態函式與基本變數之間的解析表達式代替實際的不能明確表達的結構極限狀態函式。 回響面方法是一項統計學的綜合試驗技術,用於處理幾個變數對一個體系或結構的作用問題,也就是體系或結構的輸入(變數值)與輸出(回響)的轉換關係問題。現用兩個變數來說明:結構回響Z與變數x1,x2具有未知的、不能明確表達的函式關係Z=g(x1,x2)。要得到“真實”的函式通常需要大量的模擬,而回響面法則是用有限的試驗來回歸擬合一個關係Z= g’(x1,x2),並以此來代替真實曲面Z=g(x1,x2),將功能函式表示成基本隨機變數的顯示函式,套用於可靠度分析中。 回響面方法實際上源於一種試驗設計方法,試驗設計方法是用來研究設計參數對模型設計狀況影響的一種取樣策略,決定了構造近似模型所需樣本點的個數和這些點的空間分布情況。目前廣泛套用於計算機仿真試驗設計的主要方法是拉丁超立方體抽樣和均勻設計,這兩種試驗設計能套用於多種多樣的模型,且對模型的變化具有穩健性。
回響面分析
在多因素數量處理試驗的分析中,可以分析試驗指標(因變數)與多個試驗因素(自變數)間的回歸關係,這種回歸可能是曲線或曲面的關係,因而稱為回響面分析。例如農作物產量與氮肥、磷肥、鉀肥的施肥量有關,可以通過回歸分析建立產量與施肥要素間的回歸關係,從而求得最佳施肥配方。
在回歸分析中,觀察值可以表述為:其中是自變數的函式,是誤差項。
在回響面分析中,首先要得到回歸方程 ,然後通過對自變數 的合理取值,求得最優值,這就是回響面分析的目的。