概念釋義
啟發式策略可以通過指導搜尋向最有希望的方向前進,降低了複雜性。通過刪除某些狀態及其延伸,啟發式算法可以消除組合爆炸,並得到令人能接受的解(通常並不一定是最佳解)。
然而,啟發式策略是極易出錯的。在解決問題的過程中啟發僅僅是下一步將要採取措施的一個猜想,常常根據經驗和直覺來判斷。由於啟發式搜尋只有有限的信息(比如當前狀態的描述),要想預測進一步搜尋過程中狀態空間的具體行為則很難。一個啟發式搜尋可能得到一個次最佳解,也可能一無所獲。這是啟發式搜尋固有的局限性。這種局限性不可能由所謂更好的啟發式策略或更有效的搜尋算法來消除。一般說來,啟發信息越強,擴展的無用節點就越少。引入強的啟發信息,有可能大大降低搜尋工作量,但不能保證找到最小耗散值的解路徑(最佳路徑)。因此,在實際套用中,最好能引入降低搜尋工作量的啟發信息而不犧牲找到最佳路徑的保證。
估價函式
用於評價節點重要性的函式稱為估價函式,其一般形式為
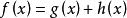 啟發式搜尋
啟發式搜尋式中:g(x)為從初始節點到節點x付出的實際代價;h(x)為從節點x到目標節點的最優路徑的估計代價。啟發性信息主要體現在h(x)中,其形式要根據問題的特性來確定。
雖然啟發式搜尋有望能夠很快到達目標節點,但需要花費一些時間來對新生節點進行評價。因此,在啟發式搜尋中,估計函式的定義是十分重要的。如定義不當,則上述搜尋算法不一定能找到問題的解,即使找到解,也不一定是最優的。
有序搜尋算法
(A算法)
在啟發式搜尋算法中,根據估價函式值,按由小到大的次序對Open表中的節點進行重新排序,這就是有序搜尋法。因此,此時的Open表是一個按節點的啟發估價函式值的大小為序排列的一個優先隊。
有序搜尋算法如下:
①將初始節點S放入Open表中;
②如Open表為空,則搜尋失敗,退出;
③把Open表的第一個節點取出,放入到Closed表中,並把該節點記為節點n;
④如果節點n是目標節點,則搜尋成功,求得一個解,退出;
⑤擴展節點n,生成一組子節點,對既不在Open表中也不在Closed表中的子節點,計算出
相應的估價函式值;
⑥把節點n的子節點放到Open表中;
⑦對Open表中的各節點按估價函式值從小到大排列;
⑧轉到②。
對上述算法分析可以發現,如果取估價函式等於節點深度,則它將退化為廣度優先搜尋。
A*算法
在A*算法中,啟發性信息用一個特別的估價函式f*來表示:f*(x)=g*(x)+h*(x)
式中:g*(x)為從初始節點到節點x的最佳路徑所付出的代價;h*(x)是從x到目標節點的最佳路徑所付出的代價;f*(x)是從初始節點出發通過節點x到達目標節點的最佳路徑的總代價。
基於上述g*(x)和h*(x)的定義,對啟發式搜尋算法中的g(x)和h(x)做如下限制:
①g(x)是對g*(x)的估計,且g(x)>0;
②h(x)是h*(x)的下界,即對任意節點x均有h(x)≤h*(x)。
在滿足上述條件情況下的有序搜尋算法稱為A*算法。
對於某一搜尋算法,當最佳路徑存在時,就一定能找到它,則稱此算法是可納的。可以證明,A*算法是可納算法。也就是說,對於有序搜尋算法,當滿足h(x)≤h*(x)條件時,只要最佳路徑存在,就一定能找出這條路徑。

