介紹
哈特倒置器的反轉器是兩種機構中的一種，它提供了完美的直線運動而沒有滑動導軌。
它們是由Harry Hart於1874-5發明並出版的。哈特倒置器的第一個反轉器基於反平行四邊形。 增加固定點和驅動臂使其成為6桿連桿。它可用於通過將一個點固定在一個短鏈路上並在另一個鏈路上以圓弧方式驅動一個點來將旋轉運動轉換為完美的直線。
哈特倒置器的第二個反轉器，也被稱為“Hart的A型框架”，其尺寸不太靈活，但具有運動垂直平分固定基點的有用特性。
哈特倒置器是由哈利·哈特在1874至1875年發明，也在同一年發表。是以反平行四邊形為基礎。
哈特倒置器可以將旋轉的運動轉換為真正的直線運動 ，需要以其中一個短桿上的一端為固定點，另一端點進行圓周運動（其固定點及驅動臂使其變成六桿機構。）
Hart的連桿
與Peaucellier連桿類似，Hart的連桿（Hart的反轉器或Hart的單元）採用反轉來在圓形和直線運動之間進行轉換。與Peaucellier連桿相比，Hart的設備使用更少的桿。
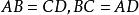哈特倒置器該裝置由四個桿AB，BC，CD和AD組成，使得 並且AD和BC相交。 AB，AD和BC上的O，P，Q滿足
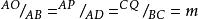哈特倒置器（1） ，
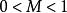哈特倒置器
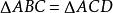哈特倒置器對於 ，在ΔABD中，（1）表示OP || BD。同樣，在ΔABC中，AQ || AC。由於對稱性，或者由於），四邊形ABDC是等腰梯形，因此BD || AC。然後從（1）得出三個點O，P，Q是共線的並且屬於與AC和BD平行的線。
稍後將證明配置的以下屬性：
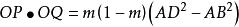哈特倒置器（2） 。
它表明P和Q在與中心O的反演下是相互反向的。這意味著，如果O是固定的並且P跟蹤曲線，Q將跟蹤曲線的反轉圖像。如果附加的桿SP如此附著在那個配置上
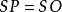哈特倒置器（3）
並且S是固定的，那么P將跟蹤穿過反轉中心O的圓。因此，Q將描述直線的一段。
下面的小程式演示了這個屬性。為了定義（或重新定義）配置的屬性，點A，B，D，O和S是可拖動的。但是，當拖動P時，O和S都保持固定。
注意，桿的尺寸對桿的相對位置施加了某些限制。當拖動P時即將違反這些內容時，小程式將停止跟蹤這些點。如果發生這種情況，請將P返回已繪製的弧並從此處重新配置。
例子
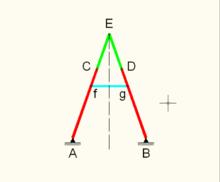圖1尺寸：
AB = 4 ，AC = BD = 4 ，CE = ED = 2 ，Af = Bg = 3 ，fC = gD = 1 ，fg = 2。
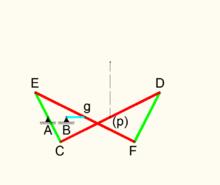圖2尺寸：
AB = Bg = 2 ，AC = AE = 3 ，CD = EF = 12 ，EC = FD = 6 ，Cp = pD = 6 ，Eg = 6。
相關條目
•直線運動機構
•平面四桿機構
