運算因素
 向量分析
向量分析向量分析中3個重要的運算:
梯度:量度標量場改變的速度與方向;標量場的斜度是個向量。
鏇度:量度向量場傾向繞著一個點鏇轉的程度;向量的捲曲是個向量場。
散度(divergence):量度向量場傾向源於一點的程度。
Stokes'theorem
同源理論
運算套用
與向量函式有關的微積分運算及其套用。
向量函式的微分法
設有一依賴於某變數t的向量函式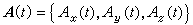 (t在某一區間α≤t≤β上變化)。如果下面這極限存在,則稱
(t在某一區間α≤t≤β上變化)。如果下面這極限存在,則稱
為A(t)在t處的導數。導數存在的充分必要條件是三個分量函式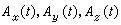 在t處都有導數,且恆有也可定義向量函式的微分:或即類似地可定義向量函式的高階導數與高階微分。
在t處都有導數,且恆有也可定義向量函式的微分:或即類似地可定義向量函式的高階導數與高階微分。
如向量函式依賴於多個自變數,例如A(u,v),則也可定義偏導數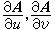 以及全微分等等。
以及全微分等等。
向量函式的積分法 A(t)在區間【α,β】上的積分定義為式中Δ為【α,β】的一分劃: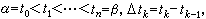
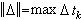 ,而τk為
,而τk為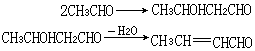 中任何一點。用分量寫法,則有
中任何一點。用分量寫法,則有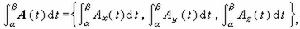 當然要假定各分量的積分存在。
當然要假定各分量的積分存在。
也可以定義重積分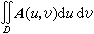 以及線積分、面積分等等。
以及線積分、面積分等等。
總之,向量函式的微分法與積分法都可通過它的各分量的相應運算來實現。
設A(t)為一曲線C上動點的位置向量,t為流動參數,亦即,C有參數方程,則A┡(t)的方向就和曲線C在t處的切線方向相同。如果A(u,v)是一曲面S上動點的位置向量,而u,v為流動參數,則向量積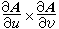 的方向就和曲面S上(u,v)處的法線方向相同。用這些基本事實,可以來研究空間曲線、曲面的性質,也是微分幾何的出發點。
的方向就和曲面S上(u,v)處的法線方向相同。用這些基本事實,可以來研究空間曲線、曲面的性質,也是微分幾何的出發點。
![向量分析[數學概念] 向量分析[數學概念]](/img/a/264/nBnauM3XyIzN1EzMxAzNzQDN3QTM4ITM0IDMxADMwAzMwIzLwczLyAzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg)
