研究歷程
關於拓撲空間可度量化的充分必要條件的探索是一般拓撲學中最古老、產生問題最多的課題之一。
亞歷山德羅夫(Александров,П.С.)和烏雷松(Урысон,П.С.)早於1923年用開覆蓋列上的一個特殊條件提供了一個答案,大約在10年後,穆爾(Moore,R.L.)稍微改變了他們的條件,瓊斯(Jones,F.B.)於1937年稱這樣的空間為穆爾空間。度量空間是穆爾空間,反之未必成立,於是,關於可度量化定理的研究轉變為精確地確定什麼樣的穆爾空間是可度量化的。
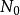 可度量化空間
可度量化空間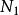 可度量化空間
可度量化空間最有名的猜測是每個正規穆爾空間是可度量化的,最近50年裡對這個猜測的研究在一般拓撲學的發展中起著重要的作用。瓊斯於1937年指出,若2 <2,則每個可分正規穆爾空間是可度量化的。賓(Bing,R.H.)和永見(Nagami,K.)指出每個仿緊穆爾空間是可度量化的。西爾弗(Silver,J.H.)於1970年用科恩模型指出正規穆爾空間猜測本身不能用現有的集論公理證明,周浩旋於1979年在附加集論假設MA+CH下,證明了存在不可度量化的穆爾空間.由此可見,可度量化問題的研究與公理集合論有密切的聯繫。
實例說明
定義
一個拓撲空間稱為是可度量化的,如果它的拓撲可以由它的某一個度量誘導出來。
 可度量化空間
可度量化空間 可度量化空間
可度量化空間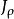 可度量化空間
可度量化空間 可度量化空間
可度量化空間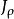 可度量化空間
可度量化空間 可度量化空間
可度量化空間設(X, )是拓撲空間,若存在集合X上的一個度量ρ使得 即是由集合X上的度量ρ誘導的拓撲 ,即 = ,則稱(X, )為可度量化空間。
舉例
例1設X是非空集,定義映射如下:
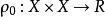 可度量化空間
可度量化空間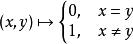 可度量化空間
可度量化空間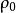 可度量化空間
可度量化空間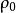 可度量化空間
可度量化空間則易證 是集合X上的度量,稱為集合X上的離散度量,(X, )稱為離散度量空間。
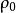 可度量化空間
可度量化空間 可度量化空間
可度量化空間 可度量化空間
可度量化空間在離散度量空間(X, )中,對於 ∈X, 的球形鄰域
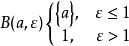 可度量化空間
可度量化空間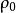 可度量化空間
可度量化空間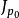 可度量化空間
可度量化空間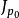 可度量化空間
可度量化空間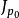 可度量化空間
可度量化空間因此B={{x}∣x∈X}是集合X上的離散度量 誘導的拓撲 的基。由於集合X的每一單點集都是這一拓撲 的開集,所以 是集合X上的離散拓撲。
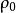 可度量化空間
可度量化空間例1表明,非空集X上的離散拓撲可由上述離散度量 誘導出,所以離散拓撲空間是可度量化空間。
例2 設X={a,b},若在集合X上賦予平凡拓撲,則此平凡拓撲空間X是不可度量化空間。
 可度量化空間
可度量化空間事實上,若平凡拓撲空間X={a,b}是可度量化空間,則存在集合X上的度量ρ,使得由其誘導的集合X上的拓撲是平凡拓撲{ ,x}.因為ρ(a,b)>0,取
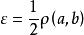 可度量化空間
可度量化空間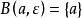 可度量化空間
可度量化空間則,所以{a}是開集,這與X是平凡空間矛盾。
相關定理
定理1 (Urysohn嵌入定理) 每一個滿足第二可數性公理的T₃空間都同胚於Hilbert空間Η的某一個子空間。
定理2 Hilbert空間H是一個可分空間。
定理3 設X是一個拓撲空間,則下列條件等價:
(1)X是一個滿足第二可數性公理的T₃空間;
(2)X同胚於Hilbert空間H的某一個子空間;
(3)X是一個可分的可度量化空間。
 可度量化空間
可度量化空間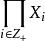 可度量化空間
可度量化空間定理4 設 是可度量化空間的一個可數族,則積空間 是一個可度量化空間。

