基本介紹
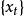 反覆殘差法
反覆殘差法雙線性差分方程 對零均值時序 擬合的雙線性模型為 :
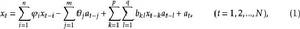 反覆殘差法
反覆殘差法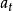 反覆殘差法
反覆殘差法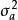 反覆殘差法
反覆殘差法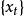 反覆殘差法
反覆殘差法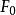 反覆殘差法
反覆殘差法記該模型為BM(n,m,p,q),其中,殘差 為方差是 的白噪聲,當 是非零均值時,上式中還應有一常數項 。
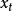 反覆殘差法
反覆殘差法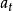 反覆殘差法
反覆殘差法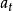 反覆殘差法
反覆殘差法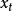 反覆殘差法
反覆殘差法式(1)較ARMA (n, m)模型多一個雙線性項,即當 固定時,變成關於 的線性模型,當 固定時,變成了關於 的線性模型,因而稱之為雙線性模型。可以把雙線性模型視為ARMA模型的推廣。但是,由於它是非線性模型,模型的定階準則,穩定性與可逆性等比ARMA模型的複雜得多,計算也困難得多。對某些較簡單的雙線性模型,建模時可沿用線性系統的定階準則,如F檢驗,AIC準則等。
在階數已確定的情況下,對於雙線性模型的參數估計問題,原則上與線性模型的處理方法相同,現敘述如下,在式(1)中,當N足夠大時,有似然函式,
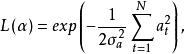 反覆殘差法
反覆殘差法 反覆殘差法
反覆殘差法式中, 為參數的集合,
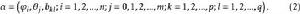 反覆殘差法
反覆殘差法 反覆殘差法
反覆殘差法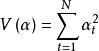 反覆殘差法
反覆殘差法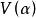 反覆殘差法
反覆殘差法 反覆殘差法
反覆殘差法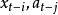 反覆殘差法
反覆殘差法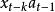 反覆殘差法
反覆殘差法 反覆殘差法
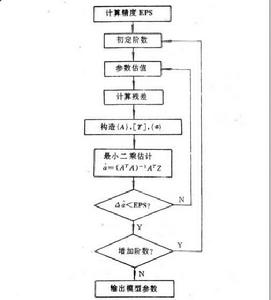
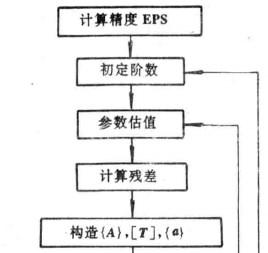
反覆殘差法於是, 的極大似然估計為使殘差平方和 達最小,即 對 中每個元素取極小化而得到,因此,關於ARMA模型的建模方法如Levinson算法一般均適用於雙線性建模。Subba Rao提出的“ 反覆殘差法”對較為簡單的雙線性建模頗為方便有效,其思路可由圖1說明。圖中Z是由{x}中的元素構成的列向量,A是 與 所構成的己知的常數矩陣, 是式(2)所示的模型參數構成的列向量,反覆殘差法是在模型階數已知的條件下建模。
 反覆殘差法 反覆殘差法 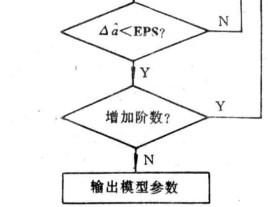 反覆殘差法 反覆殘差法 |
實例分析
下面是一個簡單的雙線性模型的建模過程。
設要建立的雙線性模型為:
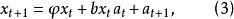 反覆殘差法
反覆殘差法即
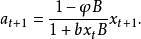 反覆殘差法
反覆殘差法式中,B為後移運算元,當b較小時,近似地有
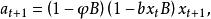 反覆殘差法
反覆殘差法即
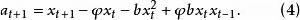 反覆殘差法
反覆殘差法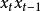 反覆殘差法
反覆殘差法忽略 項,則有
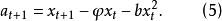 反覆殘差法
反覆殘差法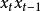 反覆殘差法
反覆殘差法於是可套用最小二乘法估計參數φ、 b,如不忽略 項,則可套用非線性最小二乘法估計參數。
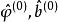 反覆殘差法
反覆殘差法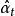 反覆殘差法
反覆殘差法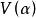 反覆殘差法
反覆殘差法設參數的初始估值為 , 則由式(5)可得其殘差的初值 ,根據式(3) 求殘差平方和 。
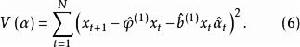 反覆殘差法
反覆殘差法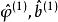 反覆殘差法
反覆殘差法在最小二乘意義下使其極小化,估計新的參數值 ,再將新參數代入式( 3)求殘差,
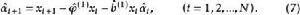 反覆殘差法
反覆殘差法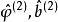 反覆殘差法
反覆殘差法求出新的殘差後,再代入式(6),估計新的參數 ,如此反覆疊代,直到滿足精度為止。
仿真建模實例
設雙線性差分方程為:
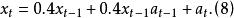 反覆殘差法
反覆殘差法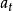 反覆殘差法
反覆殘差法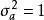 反覆殘差法
反覆殘差法圖1所示為該雙線性系統的時間序列,系統的輸入 是方差 的零均值的白噪聲,圖2所示為雙線性時序的機率密度分布圖,其中虛線為實際分布,實線為常態分配,可見該序列已不是常態分配;圖中示出了序列的均值、方差、偏態值與峰態值,從中也可看出其非線性的特性。表1列出了雙線性建模的結果。其中,F為模型中含有的常數項,以便於擬合均值不為零的時序,將表中結果與式(8) 比較可知,兩者符合情況較好,表明反覆殘差法建模是有效的。
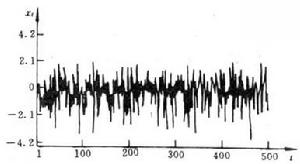 圖1 雙線性時間序列
圖1 雙線性時間序列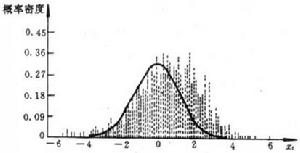 圖2 雙線性序列的機率密度分布
圖2 雙線性序列的機率密度分布均值:-0.317177 偏態:-0.347777 方差:1.543746 峰態:1. 005134
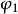 反覆殘差法 反覆殘差法 | 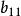 反覆殘差法 反覆殘差法 | 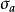 反覆殘差法 反覆殘差法 | AIC值 | EPS | F |
| 0.409 | 0.401 | 0.856 | -0.3 | 0.001 | 5. 056X 10 |