背景
近三十多年來，數學物理反問題已成為套用數學中發展和成長最快的領域之一，之所以如此在很大程度上是受其他學科與眾多工程技術領域的套用中產生的迫切需求所驅動。在實踐中，許多反問題可歸結為第一類運算元方程;而反問題的某些求解方法，例如脈衝譜技術(PST)或廣義脈衝譜技術(GPST)及最佳攝動量法等，也常常包含以第一類運算元方程的求解作為一個子過程。
反問題
顧名思義，反問題是相對於正問題而言的。以前面所舉的“盲人聽鼓”反問題為例，它的正問題就是要在已知鼓的形狀的條件下，研究其發聲規律，這在數學物理歷史上已經研究在先，而且比較成熟。此時鼓的所有譜都能通過一套算法利用計算機算出來。如何區分某個問題的“正”“反”？這並沒有一個嚴格的標準，但是我們可以粗略地這樣理解：世間的事物或現象之間往往存在著一定的自然順序，如時間順序、空間順序、因果順序，等等。所謂正問題，一般是按著這種自然順序來研究事物的演化過程或分布形態，起著由因推果的作用。反問題則是根據事物的演化結果，由可觀測的現象來探求事物的內部規律或所受的外部影響，由表及里，索隱探秘，起著倒果求因的作用。可以看出，正、反兩方面都是科學研究的重要內容。
在遙測和勘探技術中提出了大量的反問題。例如，在地球物理勘探中，通過地震波的測量來判斷地球內部的結構或地下礦藏的位置;在無損探傷中,用紅外線掃描來探測固體材料中的缺陷；通過測量地面上的牛頓引力勢來推斷地下金屬礦藏的位置、形狀和密度;利用X光分層掃描構像來作醫學診斷等等，都是在研究對象不能達到或直接接觸的情況下，利用特定的物理手段來取得有關解的某些信息，而化為數學上的反問題來處理的。工程技術中的定向設計及系統識別等方面的問題，都屬於反問題的範疇。在量子物理中，利用散射資料來反推位勢的反散射問題，也是一類有重要意義的反問題。
反問題的提法多種多樣，且往往在經典的意義下是不適定的。為了求解各種不同形式的反問題，人們已經提出了一些有效的方法，如拉東變換、反散射方法、最優設計方法以及各種正則化方法等，但是還有很多問題有待進一步的研究。
定義
反問題方法是相對正問題求解方法而言的。例如，正問題為已知幾何外形求解壓力或速度分布，而反問題方法就是根據給定的目標函式，如壓力或速度分布，求得對應的幾何外形的方法。
研究現狀和進展
國外關於反問題理論和方法的研究起步較早，最早期的工作可以追溯到20世紀20年代Hadamard在研究線性偏微分方程的Cauchy問題時對反問題不適定性的陳述和研究。20世紀40年代前蘇聯院士Tikhonov率領他的工作小組開始了反問題的理論研究。終於在60年代推出了至今仍然廣泛沿用的Tikhonov、變分正則化方法。並於70年代出版了反演理論的經典專著《Solutiorrs of lll-posed Problems》 (Tikhorronov et al.，1997；中譯本《不適定問題的解法》(王秉忱譯，陳恕行校)、地質出版社、1989)，關於反演理論和方法研究的另一個方向是疊代正則化方法，該領域的典型代表是Landweber和Fridman。 以Nashed為代表的廣義逆方法是求解反演問題的又一類重要的方法，分為內逆法和外逆法。把不適定問題的正則化放在抽象的泛函空間的完整描述是Morozov的《Methods for solving IncorrectlyPosed Problems》和Croetsch的《The Theory of Tikhonoy regulation for Fredhohn Equations of the First Kind》近年來發展起來的方法有梯度型方法和Newton方法等等。
我們國家的研究工作者在反演問題的理論和方法研究方面也進行了大量的探索，最早可追溯到20世紀70年代初由中國科學院院馮康先倡導的反演問題的研究。隨後，有關反演理論和方法在相關的領域也如火如茶地展開。有對地球物理中的反問題的系統理論論述，有對波動方程反演問題的理論和算法的系統研究，有從控制和脈衝譜角度對反演問題的論述等等、特別是大量科研人員投入精力對反演問題的正則化理論進行研究和擴展，以及從最最佳化角度對反演理論和方法的研究。
正則化方法
正則化(regularization)，是指線上性代數理論中，不適定問題通常是由一組線性代數方程定義的，而且這組方程組通常來源於有著很大的條件數的不適定反問題。大條件數意味著捨入誤差或其它誤差會嚴重地影響問題的結果。
求解不適定問題的普遍方法是:用一組與原不適定問題相“鄰近”的適定問題的解去逼近原問題的解,這種方法稱為正則化方法。如何建立有效的正則化方法是反問題領域中不適定問題研究的重要內容。通常的正則化方法有基於變分原理的Tikhonov 正則化、各種疊代方法以及其它的一些改進方法,這些方法都是求解不適定問題的有效方法,在各類反問題的研究中被廣泛採用，並得到深入研究。
壓氣機葉片反問題設計
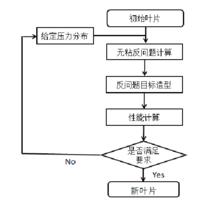壓氣機葉片無粘反問題設計流程反問題設計方法通過給定特定流場參數分布，根據流場參數和幾何參數之間的關係求解葉片造型，具有較高的設計效率。馮·卡門研究所發展出基於滲透邊界的葉片反問題設計方法，給定葉片吸力面和壓力面壓力分布，反問題計算過程中葉片表面出現滲透速度，在計算收斂的流場中追蹤流線實現對新氣動型面的求解，以軸流壓氣機葉片和渦輪葉片為算例驗證了其有效性。
葉輪機械內部巨觀流動的主要驅動力是壓力場，葉表靜壓直觀地反映葉片段的負荷分布，以葉片吸力面、壓力面表面壓力分布作為給定參數，可實現對葉表流動狀態的直接控制。從初始葉片出發，以葉片表面壓力作為給定參數的壓氣機葉片無粘反問題設計流程如下:
1)給定初始葉片及目標壓力分布;
2)基於可滲透壁面邊界條件的無粘反問題流場計算;
3)反問題目標葉片求解，在反問題流場中計算葉片修正量，得到目標葉片;
4)對目標葉片進行性能計算，葉片表面為固壁邊界條件，如果不滿足性能要求，則以此葉片作為初始葉片返回至第1}步再進行以上過程，直至得到的新葉片滿足目標性能要求。
該反問題方法的主要設計步驟包括基於可滲透壁面邊界條件的CFD流場計算和基於流線追蹤的壁面求解。無粘正問題計算過程中壁面採用無粘滑移邊界條件，葉片表面被視為無流體穿過的物理邊界，邊界上流體的法向速度為零，僅存在切向流動;無粘反問題計算過程中壁面採用可滲透壁面邊界條件，葉片表面被視為流體可穿過的數值邊界，邊界上流體的法向速度不再必然為零，其方向和數值由流動狀態和給定壓力的關係決定，從而形成與邊界幾何上不一致的近壁流線。
流線追蹤過程從前緣滯止點出發，基於單元體質量守恆原理求解流線。對於軸流壓氣機葉片，在正問題無粘流場中，貼體流線與壁面吻合較好;反問題流場中由於壁面法向速度的存在，近壁面流線不再與壁面重合，可基於此原理追蹤從前緣滯止點出發的流線(或流面)，以此作為與給定壓力分布相匹配的新葉片壁面可實現反問題設計。
