數學
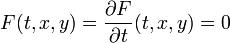包絡線所滿足的方程在數學上，一族平面直線（或曲線）的“包絡”（envelope）是指一條與這族直線（或曲線）中任意一條都相切的曲線。假設這族平面曲線記為F（t，x，y），這裡不同的t 對應著曲線族中不同的曲線，則包絡線上的每一點滿足右下端的兩條方程，由這兩條方程消去t後便可得出包絡線的隱式表示。
包絡線類似地可以定義空間中一族平面（或曲面）的包絡。
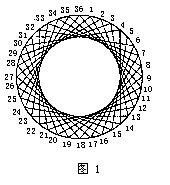
如圖1中的直線組成一個圈，然而實際上我們並沒有“畫”這個圓，這時就把這個圓稱作是包絡線。
要想畫出類似的包絡線，首先要畫出一個大圓（例如直徑10cm），並把圓周分成36等分，用量角器每10°作一點即可。
把第n點與第n+10點連線，就可畫出圓形包絡線。如果n+10大於36，則須減去36。例如當n=29時，n+10=39，減去36之後得到3，所以第29點是與第3點連線。
信號處理中的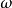包絡
包絡我們可以將任一平穩窄帶實高斯隨機過程X(t)表示為準正態振盪的形式
：
X(t)=A(t)cos(
t+
(t))
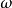包絡其中
是窄帶隨機過程的載波頻率；A(t)和
(t)是X(t)的包絡和相位。包絡即隨機過程的振幅隨著時間變化的曲線。
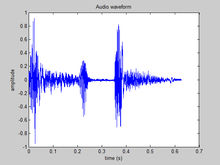QQ系統提示音的時間振幅圖像經濟學
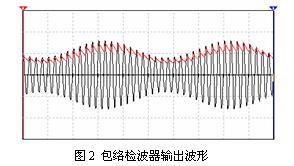波形這裡主要指的是包絡定理，西方經濟學中套用在分析廠家長期成產成本函式等的理論工具 。
它的內容是考慮含參量a的函式f（x，a）的無條件極值問題（x是內生變數，a是外生變數）。顯然，一般地其最優解V是參量a的函式，即V（a）。
包絡定理指出：V對a的導數等於f對a的偏導數（注意是f對“a所在位”變數的偏導數）。
文學
1、意為包圍環繞。
《徐霞客遊記》語見於宋·蘇軾《表忠觀碑》：“大城其居，包絡山川，左江右湖，控制島巒。” 宋·趙希鵠《洞天清錄·古硯辨》：“ 端溪中巖舊坑，石色紫，如新嫩肝，細潤如玉……外有黃臕包絡，扣之無甚聲，磨墨亦無聲。” 明·徐弘祖《徐霞客遊記·滇游日記八》：“其內水兩重，皆西轉而北去，其外大水逆兜，獨南流而東繞，此諸流包絡之分也。” 清·趙翼《蛛網》詩：“區區設罻羅，包絡能幾尺。”
2、意為猶包括。
元·柳貫《尊經堂》詩：“貞明配日月，廣大侔天地，簡牘之所資，包絡無巨細。” 清·沈德潛 《說詩晬語》卷下：“ 杜詩別於諸家，在包絡一切，其時露缺處，正是無所不有處。” 章炳麟《國故論衡·文學總略》：“凡雲文者，包絡一切箸於竹帛者而為言。”
中醫
中醫 脈絡分布中醫裡面是指周身脈絡。
《醫宗金鑒·痘疹心法要訣·痘主部位》：“包絡之絡聯藏府，三焦之氣應無方。”註：“至於包絡，乃周身脂膜之絡，聯屬百骸藏府者也。”
