簡介
所謂動穩性指船舶在動態外力矩作用下計及橫傾角加速度和慣性矩的穩性。
在討論船舶靜穩性時,通常假設力矩逐漸作用於船上,使外力矩與靜穩性力矩處處平衡,因而不需考慮船舶橫傾過程中的角加速度和慣性矩。船舶在海上航行中時常受到外力矩的突然作用,如陣風的突然襲擊、海浪的猛烈衝擊、拖輪急拖或急頂等,此類外力矩在較短時間內有明顯變化或突然作用於船上,則應計及橫傾過程中的角加速度和慣性矩。
船舶動平衡及動傾角
如圖1所示,船舶初始為正浮狀態,然後受一定常動態外力矩M作用,此時作用於船舶的合力矩M為
 動穩性
動穩性 圖1
圖1設外力矩M做功以W表示,穩性力矩M做功以W表示,它們在數值上分別等於各自曲線下的面積。船舶在橫傾過程中,只要M和M不等,即合力矩M不為0,則產生一角加速度θ″,迫使船舶作加(減)速橫傾;只要外力矩做的功W不等於穩性力矩做的功W,船舶就具有一定的角速度使船舶繼續橫傾。
船舶在動態外力矩作用下的橫搖過程可分為以下幾個階段:
1)θ=0:合力矩M最大,故橫搖角加速度θ″最大,而兩力矩作的功W=W=0,故橫搖角速度θ′=0,船舶在θ″迫使下開始橫搖;
2)0<θ<θ:合力矩M逐漸減小,因而橫搖角加速度θ″逐漸減小;而兩力矩做的功W>W,且合力矩作的功(W-W)增大,使得橫搖角速度θ′增大,船舶加速橫搖;
3)θ=θ:合力矩M=0,故橫搖角加速度θ″=0;而兩力矩作的功繼續滿足W>W,且合力矩做功(W-W)達最大值,使得橫搖角速度θ′最大,船舶在此處橫搖最快;
4)θ>θ:合力矩M由0變為負值且逐漸增大,則橫搖角加速度θ″也由0變為負值並逐漸增大;而兩力矩作的功仍然滿足W>W,但合力矩做功(W-W)在θ>θ後逐漸減小,使得橫搖角速度θ′隨之漸減,船舶橫搖也漸緩;
5)θ=θ:合力矩M負值最大,則橫搖角加速度θ″負值達最大;而此時合力矩做的功(W-W)=0,即W=W,使得橫搖角速度θ′=0,船舶在此處因θ′=0而不再繼續向前橫搖;
6)θ<θ:合力矩M負值在θ=θ處為最大值,故θ″負值最大使得船不能停留在θ處而迫使船舶反向橫搖。這樣,船舶在M和M作用下於θ左右做下一周期的橫搖運動。
事實上,船舶在周期性橫搖過程中,由於舷外水對船舶橫搖的阻尼作用,橫搖運動的擺幅將逐漸減小,最終於θ處靜止下來。
在動態外力矩作用下船舶發生傾斜,當角速度為零時不再向傾斜方向繼續傾斜,此時船舶處於動平衡狀態。船舶達到動平衡時的橫傾角稱動平衡角(Angel of dynamical stability),簡稱動傾角,以θ表示。
由上分析可知,船舶在動態外力矩作用下達到動平衡的條件為
 動穩性
動穩性即外力矩作的功等於穩性力矩作的功時,船舶達到動平衡。在靜穩性曲線圖上,表現為面積OME等於面積EFN;兩個面積相等時其右邊界線對應橫傾角即為動傾角。
船舶動穩性大小的基本標誌
船舶在動態外力矩作用下發生傾斜,考慮了船舶傾斜過程中的角加速度和慣性矩的影響,船舶抵抗外力矩的能力不能再以穩性力矩來衡量,而是應以穩性力矩做的功來衡量。由此可見,船舶動穩性在不同裝載狀況下其大小應以穩性力矩做的功來表征。穩性力矩所做功W亦稱動穩性力矩,以M表示。
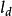 動穩性
動穩性由於動穩性力矩M在數值上等於靜穩性力矩M曲線下的面積,而M=Δ·GZ並設Δ為常量,於是定義靜穩性力臂GZ曲線下的面積為動穩性力臂(Dynamical stability lever)。則動穩性力矩M為
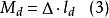 動穩性
動穩性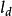 動穩性
動穩性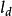 動穩性
動穩性由上式可知,在排水量一定的條件下,穩性力矩所做的功取決於動穩性力臂,並與其成正比,因此動穩性力臂可以作為船舶動穩性大小的基本標誌。
最小傾覆力矩
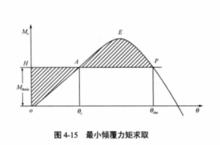 圖2
圖2在靜穩性曲線圖上,外力矩曲線下面積與穩性力矩曲線下面積相等時對應的橫傾角即為動傾角。由作圖求θ可知,當外力矩M增大時,M曲線位置提高,曲線下的面積增大。為取得動平衡,需有更多的M曲線面積抵償,則計算曲線面積時的右邊界線後移,相應的動傾角增大。如圖2所示,當外力矩M增大到某一數值時,曲線圖中坐標縱軸、M曲線及M直線所包圍的面積OHA等於M直線與M曲線所圍冠狀面積AEP,使得船舶動平衡達到極限位置。若將M值再增大時,則無論橫傾角多大,M曲線下的面積恆大於M曲線下的面積,船舶不再滿足動平衡條件,也就不存在動平衡位置。
顯而易見,從動穩性角度分析,船舶在極限動平衡時對應的外力矩為船舶能夠承受外力矩的最大能力;或者說,該外力矩是使船舶傾覆所需要的最小值。當實際外力矩大於該值時,船舶因動平衡不復存在而導致傾覆。因此,將船舶在極限動平衡時的外力矩稱為最小傾覆力矩,以M。表示。它是衡量船舶動穩性的重要參數。船舶在最小傾覆力矩作用下所對應的動傾角稱為極限動傾角,以θ表示。
從動穩性要求來考慮,保證船舶不致傾覆的條件應為
 動穩性
動穩性
