提出背景
在大部分的學科中,時間序列是數據的一種常見表示形式。對於時間序列處理來說,一個普遍的任務就是比較兩個序列的相似性。在時間序列中,需要比較相似性的兩段時間序列的長度可能並不相等,在語音識別領域表現為不同人的語速不同。
語音信號具有很強的隨機性,不同的發音習慣,發音時所處的環境不同,心情不同都會導致發音持續時間長短不一的現象。如單詞最後的聲音帶上一些拖音,或者帶上一點呼吸音,此時,由於拖音或呼吸音會被誤認為一個音素,造成單詞的端點檢測不準,造成特徵參數的變化,從而影響測度估計,降低識別率。
在孤立詞語音識別中,最為簡單有效的方法是採用動態時間歸整(Dynamic Time Warping)算法。該算法基於動態規劃(DP)的思想,解決了發音長短不一的模板匹配問題,是語音識別中出現較早、較為經典的一種算法,用於孤立詞識別。
基本概念
動態時間規整在60年代由日本學者Itakura提出,把未知量伸長或縮短(壓擴),直到與參考模板的長度一致,在這一過程中,未知單詞的時間軸會產生扭曲或彎折,以便其特徵量與標準模式對應 。
原理描述
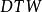 動態時間規整
動態時間規整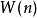 動態時間規整
動態時間規整是一個典型的最佳化問題,它用滿足一定條件的的時間規整函式 描述測試模板和參考模板的時間對應關係,求解兩模板匹配時累計距離最小所對應的規整函式。
 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整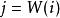 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整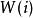 動態時間規整
動態時間規整測試語音參數共有 幀矢量,而參考模板共有 幀矢量, 和 不等,尋找一個時間規整函式 ,它將測試矢量的時間軸 非線性地映射到模板的時間軸 上,並使該函式 滿足:
 動態時間規整
動態時間規整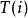 動態時間規整
動態時間規整 動態時間規整
動態時間規整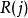 動態時間規整
動態時間規整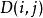 動態時間規整
動態時間規整第 幀測試矢量 和第 幀模板矢量 之間的距離測度
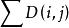 動態時間規整
動態時間規整最優時間規整情況下,所有矢量幀間的距離和 最小 。
實現步驟
 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整給定兩個時間序列 和 ,他們的長度分別是 和 :
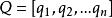 動態時間規整
動態時間規整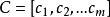 動態時間規整
動態時間規整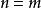 動態時間規整
動態時間規整若 ,可直接計算兩個序列的距離;
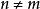 動態時間規整
動態時間規整若 ,則需要線性縮放,即把短的序列線性放大到和長序列一樣的長度,或者把長的線性縮短到和短序列一樣的長度,再進行比較。但是,語音中各個段在不同情況下的持續時間會產生或長或短的變化,因此,這樣的計算導致識別效果不佳。實踐中,更多的是採用動態規劃(dynamic programming)的方法, 具體如下:
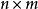 動態時間規整
動態時間規整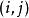 動態時間規整
動態時間規整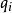 動態時間規整
動態時間規整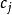 動態時間規整
動態時間規整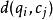 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整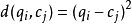 動態時間規整
動態時間規整為對齊這兩個序列,構造一個 的矩陣格線,矩陣 處的元素為 和 兩個點的距離 (即序列 的每一個點和 的每一個點之間的相似度,距離越小則相似度越高),一般採用歐式距離,即 。該DP方法可以歸結為尋找一條通過此格線中若干格點的路徑,路徑通過的格點即為兩個序列進行計算的對齊的點。
那么如何找到這條路徑?
 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整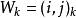 動態時間規整
動態時間規整我們把這條路徑定義為warping path 規整路徑,並用 來表示, 的第 個元素定義為 ,
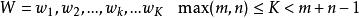 動態時間規整
動態時間規整這條路徑不是隨意選擇的,需要滿足以下幾個約束:
(1) 邊界條件:
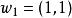 動態時間規整
動態時間規整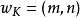 動態時間規整
動態時間規整任何一種語音的發音快慢都有可能變化,但是其各部分的先後次序不可能改變,因此所選的路徑必定是從左下角出發,在右上角結束。
(2) 連續性:
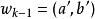 動態時間規整
動態時間規整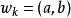 動態時間規整
動態時間規整若 ,則路徑的下一個點 需要滿足
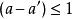 動態時間規整
動態時間規整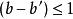 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整即,不可能跨過某個點去匹配,只能和自己相鄰的點對齊。這樣可以保證 和 中的每個坐標都在 中出現。
(3) 單調性:
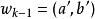 動態時間規整
動態時間規整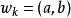 動態時間規整
動態時間規整如果 ,那么對於路徑的下一個點 需要滿足
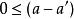 動態時間規整
動態時間規整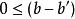 動態時間規整
動態時間規整 動態時間規整
動態時間規整這限制 上面的點必須是隨著時間單調進行的。
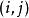 動態時間規整
動態時間規整綜合連續性和單調性約束,每一個格點的路徑就只有三個方向。如:如果路徑已經通過了格點 ,那么下一個通過的格點只可能是下列三種情況之一:
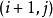 動態時間規整
動態時間規整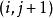 動態時間規整
動態時間規整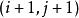 動態時間規整
動態時間規整滿足上面這些約束條件的路徑可以有指數個,然後我們感興趣的是使得下面的規整代價最小的路徑:
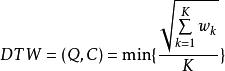 動態時間規整
動態時間規整該路徑可通過動態規划算法得到。
舉例
假設標準模板R為字母ABCDEF(6個),測試模板T為1234(4個)。R和T中各元素之間的距離已經給出。如下:
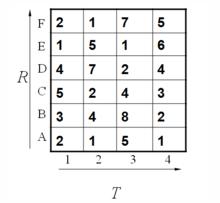 動態時間規整
動態時間規整我們需要找出其中距離最短的那條匹配路徑。
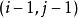 動態時間規整
動態時間規整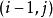 動態時間規整
動態時間規整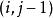 動態時間規整
動態時間規整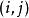 動態時間規整
動態時間規整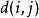 動態時間規整
動態時間規整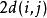 動態時間規整
動態時間規整現假設題目滿足如下的約束:當從一個方格 或 或 中到下一個方格,如果是橫著或者豎著的話其距離為,如果是斜著對角線過來的則是。其約束條件如下:
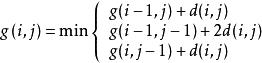 動態時間規整
動態時間規整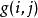 動態時間規整
動態時間規整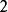 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整 動態時間規整
動態時間規整其中, 表示 個模板都從起始分量逐次匹配,已經到了 中的 分量和 中的 分量,並且匹配到該步是兩個個模板之間的距離。
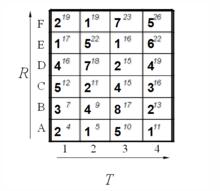
所以我們將所有的匹配步驟標註後如下:
 動態時間規整
動態時間規整路徑如下圖:
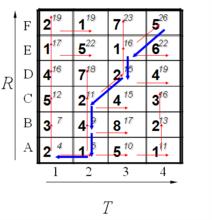 動態時間規整
動態時間規整在語音中的套用
假定一個孤立字(詞)語音識別系統,利用模板匹配法進行識別。這時一般是把整個單詞作為識別單元。在訓練階段,用戶將辭彙表中的每一個單詞說一遍,提取特徵後作為一個模板,存入模板庫。在識別階段,對一個新來的需要識別的詞,也同樣提取特徵,然後採用DTW算法和模板庫中的每一個模板進行匹配,計算距離。求出最短距離也就是最相似的那個就是識別出來的字了 。