線性動態地球系統
能夠用線性數學模型描述的動態地球系統，稱為線性動態地球系統。線性動態地球系統的基本特性，即輸出回響特性、狀態回響特性、狀態轉移特性，都滿足疊加原理。令f代表某種數學操作，如關係、變換、運算、函式、泛函、方程等，x記數學操作的對象（如變數），f（x）代表對x施加操作f的結果。
如果，f（x）滿足條件
加和性
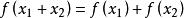動態地球系統齊次性
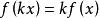動態地球系統（k為常數）
就稱數學操作f為線性的。如線性關係，線性變換，線性運算，線性函式，線性泛函，線性方程等等。將上述兩式合併表示為
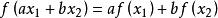動態地球系統稱為疊加原理，a，b為常數。滿足疊加原理是線性操作區別於非線性操作的基本標誌。
連續動態地球系統的數學模型是微分方程，刻畫系統的動態變數對狀態變數的依存關係以及狀態變數之間的相互影響。如果狀態變數只是時間的函式，與空間分布無關，稱為集中參數系統，用常微分方程描述。狀態變數同時依賴於時間和空間分布（同一時刻不同點的狀態變數數值不同），則稱分布參數系統，須用偏微分方程描述。
地球系統線性連續動態系統的數學模型為線性常微分方程，可以使用一元高階方程，也可以使用多元一階聯立方程組。一般來說，這兩種形式是等價的，可以互換。
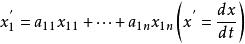動態地球系統
動態地球系統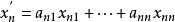
動態地球系統係數矩陣為
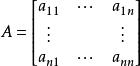動態地球系統令
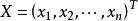動態地球系統記狀態向量，動態方程可表示為以下向量矩陣形式
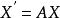動態地球系統如果係數矩陣A=（a）不隨時間而變化，即a為常數，稱為常係數方程。如果係數為時間t的函式a（t），係數矩陣記為A（t），稱為變係數方程。
數學模型有兩個基本來源：
①許多系統的非線性因素微弱，允許忽略不計，近似滿足線性假設（假設疊加原理成立），根據相關學科的基本原理直接建立線性方程；
②許多系統具有較強的非線性因素，線性假設不成立，根據基本原理只能建立非線性數學模型；但如果我們關心的主要是系統的局部性質（系統在某一點附近的行為），非線性模型又滿足連續性和光滑性要求，就可以在該點附近把它線性化，得到線性模型，可用它來近似描述地球系統的局部行為。
模型方法隱含的一個假定是，只要動力學方程是合理的，我們就認為一切有關係統行為特性信息都包含於其中，即包含於方程的結構和係數（控制參量）中。對於線性系統，這些信息都包含在係數矩陣之中。最理想的處理方法是求方程的解析解，只要求得方程的解析解，就可以把握地球系統的全部行為特性。
穩定性問題
穩定性（stability）指的是地球系統的結構、狀態、行為的恆定性，即地球系統結構、狀態、行為的抗干擾能力。穩定性是地球系統的一種重要維生機制，穩定性愈好，系統的維生能力愈強。一個狀態如果不穩定，必定是物理上不可實現（不可達）的，至多在某個動態過程中瞬間出現。一個系統的狀態空間如果沒有任何穩定定態，必定是物理上不可實現的，地球系統理論無需討論它。
從套用角度看，一個不穩定的系統無法正常運行，無法實現其功能目標，因而是沒有用的。人們總是力求採用足夠穩定的系統。但若從演化角度看，如果一個系統的所有狀態在所有條件下都是穩定的，它就沒有變化、發展、創新的可能。只有原來的狀態、結構、行為模式在一定條件下失去穩定性，系統才可能向新的結構、狀態、行為模型演化，即系統有發展創新的可能。
所以，不穩定性在地球系統演化理論中具有非常積極的、建設性的作用。但穩定是發展的前提。新狀態、新結構、新模式如果不穩定，沒有能力保存自己，它也不可能取代舊狀態、舊結構、舊模式。新系統只有具備穩定性機制，才能保持剛剛建立起來的結構和特性，保存已積累的信息。
穩定性問題是動態地球系統理論的首要問題。什麼是穩定性，如何判別穩定性，穩定性的類型，系統的穩定性程度，系統是否存在不穩定點，穩定的系統在什麼條件下會失去穩定性，如何確定系統的失穩點，系統在失穩點附近行為特性的分析，如何從失穩的原狀態向穩定的新狀態過渡等，回答這些問題形成了穩定性理論，是地球系統科學的重要內容之一。
組分關聯方式的穩定與否一般難以直接用數學方法描述，行為的描述可以歸結為狀態描述，狀態的穩定與否可以用數學方法描述。因此，動態地球系統理論的穩定性研究總是圍繞狀態以及由狀態構成的軌道這兩個概念進行的。狀態或軌道是否穩定，能夠間接表征地球系統的組分關聯方式和整體行為模式是否穩定，只要對狀態或軌道的穩定與否做出判斷。便無需再對系統結構或行為模式的穩定性問題進行研究。
