釋義
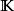 勒貝格空間
勒貝格空間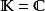 勒貝格空間
勒貝格空間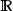 勒貝格空間
勒貝格空間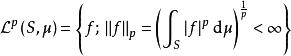 勒貝格空間
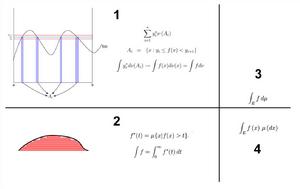
勒貝格空間當空間維度是無窮而且不可數的時候(沒有一個可數的基底),無法運用有限維或可數維度空間的辦法來定義範數,但對於可積函式空間,仍然能夠定義類似的概念。具體來說,給定可測空間( S, Σ, μ)以及大於等於1的實數 p,考慮所有從 S到域( 或 )上的可測函式。考慮所有絕對值的 p次冪在 S可積的函式,也就是集合 :
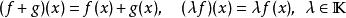 勒貝格空間
勒貝格空間集合中的函式可以進行加法和數乘:
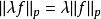 勒貝格空間
勒貝格空間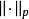 勒貝格空間
勒貝格空間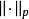 勒貝格空間
勒貝格空間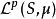 勒貝格空間
勒貝格空間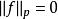 勒貝格空間
勒貝格空間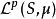 勒貝格空間
勒貝格空間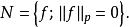 勒貝格空間
勒貝格空間從不等式:| f+ g|≤ 2(| f|+ | g|)可知,兩個 p次可積函式的和,也是一個 p次可積函式。另外,容易證明 ;閔可夫斯基不等式的積分形式說明三角不等式對 成立。滿足這樣條件的 構成一個半範數,令 成為一個半賦范向量空間。之所以是半範數,是因為滿足 的函式f不一定是零函式。然而可以通過一套標準的拓撲方法從這個半賦范空間得到一個賦范空間:考慮 中所有使得{\displaystyle \|f\|_{p}=0}的函式f的集合:
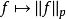 勒貝格空間
勒貝格空間集合{\displaystyle N}可以看作是映射的零空間。
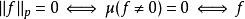 勒貝格空間
勒貝格空間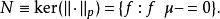 勒貝格空間
勒貝格空間對可測函式f來說, 幾乎處處為零(在測度 μ意義下)。所以
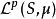 勒貝格空間
勒貝格空間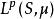 勒貝格空間
勒貝格空間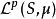 勒貝格空間
勒貝格空間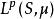 勒貝格空間
勒貝格空間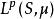 勒貝格空間
勒貝格空間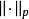 勒貝格空間
勒貝格空間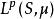 勒貝格空間
勒貝格空間而N同時也是 的一個子空間。設 是 關於N的商空間。 中的某個元素f可以看作是所有和函式f相差一個N中元素的函式構成的等價類。這樣定義的空間 是一個賦范向量空間,稱為 S上函式關於測度 μ的 L空間。 稱為 函式的 p-範數。
需要注意的是, L空間中的元素嚴格來說並不是具體的函式,而是一族函式構成的等價類。而當需要將 L空間元素當作函式來計算的時候,參與計算的實際是從這一族函式中抽取的一個代表函式。
與序列空間一樣,在函式空間上也可以定義一致範數。定義的方法和範數一樣,首先定義:
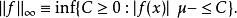 勒貝格空間
勒貝格空間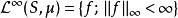 勒貝格空間
勒貝格空間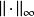 勒貝格空間
勒貝格空間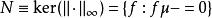 勒貝格空間
勒貝格空間 勒貝格空間
勒貝格空間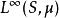 勒貝格空間
勒貝格空間是一個半範數,取 ,則 關於N的商空間是一個賦范向量空間,記作 。
一致範數與 p-範數之間存在以下關係:
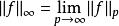 勒貝格空間
勒貝格空間可以證明, L空間是完備的空間,也即是說是一個巴拿赫空間(完備賦范向量空間)。 L空間的完備性通常被稱為里茲-費舍爾定理。具體的證明可以藉助測度上的勒貝格積分的相關收斂定理來完成。
特例
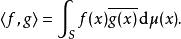 勒貝格空間
勒貝格空間L空間都是巴拿赫空間,但只有當 p= 2的時候, L空間是希爾伯特空間。也就是說,可以為 L空間中的元素定義內積。具體形式是:
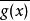 勒貝格空間
勒貝格空間其中的 表示複數的共軛。這個內積是從2-範數自然誘導的內積。 L空間在傅立葉級數和量子力學以及其他領域有著重要的運用。
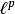 勒貝格空間
勒貝格空間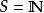 勒貝格空間
勒貝格空間 勒貝格空間
勒貝格空間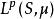 勒貝格空間
勒貝格空間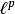 勒貝格空間
勒貝格空間空間可以看作是 L空間的特例。只要取 L空間中的 ,測度為 的計數測度,則對應的 就是 空間。
性質
對偶空間
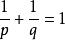 勒貝格空間
勒貝格空間一個拓撲向量空間的對偶空間是指由這個向量空間上的所有的連續線性泛函構成的泛函空間。對某個大於1的實數 p,設 q是滿足 的唯一實數,則空間 L( S, μ)的對偶空間 L( S, μ)與 L( S, μ)同構。這個關係可以通過一個自然的同構映射展現:
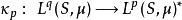 勒貝格空間
勒貝格空間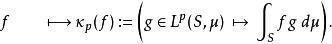 勒貝格空間
勒貝格空間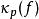 勒貝格空間
勒貝格空間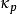 勒貝格空間
勒貝格空間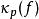 勒貝格空間
勒貝格空間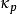 勒貝格空間
勒貝格空間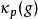 勒貝格空間
勒貝格空間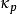 勒貝格空間
勒貝格空間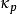 勒貝格空間
勒貝格空間赫爾德不等式保證了其中的泛函 是良好定義並且是連續的。 是一個線性映射,根據赫爾德不等式的極限情況, 作為泛函的範數和f一樣,這說明 是一個等距映射。此外還可以證明,對偶空間 L( S, μ)中的任一線性泛函對偶空間 G都能表示成某個 的形式,所以是一個滿射。結合以上性質可以推出,是一個等距同構。在這個同構的意義下,我們常說 L( S, μ)的對偶空間“是” L( S, μ)。
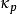 勒貝格空間
勒貝格空間以上性質說明,當大於1的時候, L( S, μ)是一個自反空間: L( S, μ)的二次對偶空間(對偶空間的對偶空間)“是”它自己(在同構的意義下)。具體來說,從 出發,可以構造出以下的關係:
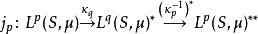 勒貝格空間
勒貝格空間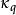 勒貝格空間
勒貝格空間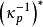 勒貝格空間
勒貝格空間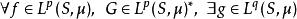 勒貝格空間
勒貝格空間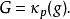 勒貝格空間
勒貝格空間與 的複合映射 j是從 L( S, μ)映射到其二次對偶空間的賦值嵌入映射: 使得
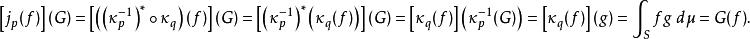 勒貝格空間
勒貝格空間從而 作為兩個等距同構的複合映射, j也是等距同構。這說明 L( S, μ)和 L( S, μ)也是同構關係。
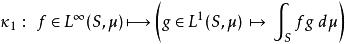 勒貝格空間
勒貝格空間如果測度 μ是σ-有限測度,那么 L( S, μ)和 L( S, μ)也是等距同構。可以證明,
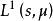 勒貝格空間
勒貝格空間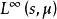 勒貝格空間
勒貝格空間是 到 上的一個同構。
嵌入
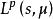 勒貝格空間
勒貝格空間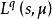 勒貝格空間
勒貝格空間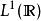 勒貝格空間
勒貝格空間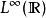 勒貝格空間
勒貝格空間給定兩個實數:1 ≤ p< q≤ ∞,當比較 和 的時候會發現,前者中包含一些局部行為更加不規則的函式,而後者中則包含了“尾巴更粗”的函式。舉例來說, 中的連續函式(也就是實數域上的勒貝格可積函式)可以在0的附近取很大的值,但當自變數趨於無窮大的時候,函式的值必須趨於0. 而對於 中的連續函式(有界連續函式),無論自變數多大,函式值都可以不在0附近,但反過來說,無論自變數取多少,函式的值也不能超過上界和下界。
假設全集 S在 μ中的測度有限,以及1 ≤ p< q≤ ∞。那么由赫爾德不等式有如下限制:
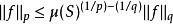 勒貝格空間
勒貝格空間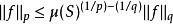 勒貝格空間
勒貝格空間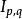 勒貝格空間
勒貝格空間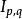 勒貝格空間
勒貝格空間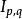 勒貝格空間
勒貝格空間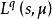 勒貝格空間
勒貝格空間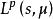 勒貝格空間
勒貝格空間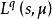 勒貝格空間
勒貝格空間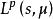 勒貝格空間
勒貝格空間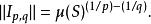 勒貝格空間
勒貝格空間這說明空間 可以被連續地嵌入到 裡面。換句話說, 到 上的恆等映射是有界連續映射。的運算元範數就是由以上不等式取等號的情形確定的:
稠密子空間
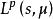 勒貝格空間
勒貝格空間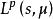 勒貝格空間
勒貝格空間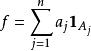 勒貝格空間
勒貝格空間研究某個複雜的無窮維賦范空間的時候,常常會使用一個由空間中比較“簡單”的元素構成的稠密子集來逼近空間中的一個元素。假設1≤ p< ∞,則空間 L( S, μ)中的元素可以用測度空間( S, Σ, μ) 上的 簡單可積函式逼近。給定測度空間( S, Σ, μ),其上的一個簡單可積函式指的是形同: 的函式。其中的 a是實數或複數係數, A∈ Σ 是測度有限的可測集合。由勒貝格積分的構造方法可知,簡單可積函式的集合在中稠密。
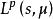 勒貝格空間
勒貝格空間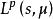 勒貝格空間
勒貝格空間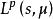 勒貝格空間
勒貝格空間如果 S本身也是測度空間,而 μ是 S上的博雷爾測度,那么可以通過烏雷松引理證明,所有 S可測而且測度有限的子集對應的指示函式都可以通過連續函式逼近。所以所有的簡單可積函式可以用連續函式逼近。因而可以證明, 中的連續函式構成的集合在 中稠密。對於更具體的空間,可以證明更加強的結果。比如說當 S是 n維歐幾里德空間,而 μ是 S上的正則博雷爾測度的時候,可以證明,所有緊支撐的光滑函式的集合在( 中稠密。