簡介
像差理論:對像差的性質,像差和光學系統結構參數的關係,進行了長期的研究,取得了很多有價值的成果。把像差和y,h的關係用冪級數形式表示。最低次冪對應的像差叫做初級像差。較高次冪對應的像差叫做高級像差。
歷史
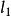 初級象差
初級象差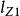 初級象差
初級象差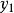 初級象差
初級象差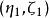 初級象差
初級象差1856年,慕尼黑天文學家賽德首先提出具有對稱軸的光學系統的初級像差理論。對於已知結構(r、d、n)的光學系統,當物距( )和入瞳位置( )給定時,光學系統的空間光線像差僅決定於視場( )、孔徑。像差展開為級數時,視場和孔徑為0,像差也為0,故展開式中不應有常數項。
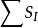 初級象差
初級象差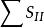 初級象差
初級象差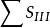 初級象差
初級象差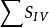 初級象差
初級象差 初級象差
初級象差賽德推出僅有5 種獨立的初級像差,即以和數(初級球差),(初級彗差),(初級像散),(初級場曲),(初級畸變)。常把這5個和數稱為第一、二、三、四、五賽德和數,5種初級像差稱為賽德像差,它們有意義的區域稱為賽德區。
空間光線的像差展開成級數時,除了初級像差還有高級像差。以垂軸像差為例,設係數中的因子為:
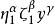 初級象差
初級象差令 :K =α+β+γ,K = 3 為初級像差;K = 5 為二級像差;K = 7 為三級像差,… 。不同級次的像差的獨立像差數目不同,獨立像差的個數可按下式計算:
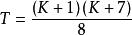 初級象差
初級象差可知二級像差有9 種獨立像差,三級像差有14 種獨立像差,依次類推。
五種初級像差
五個賽德和數
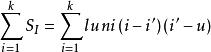 初級象差
初級象差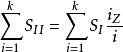 初級象差
初級象差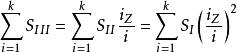 初級象差
初級象差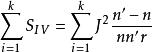 初級象差
初級象差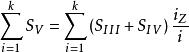 初級象差
初級象差初級像差的一般表達式具有普遍意義,可以用來導出5種初級像差的和數式。
初級球差
 初級象差
初級象差當物高y= 0 時,軸向像差ΔL'即球差L'。由於軸上點發出的光束對稱於光軸,利用子午面內的一條邊緣光線的坐標(η= ρ,y= 0,ζ = 0),簡化得:
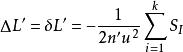 初級象差
初級象差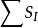 初級象差
初級象差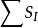 初級象差
初級象差即初級球差公式。第一賽德和數表征了球差的存在、符號和數量的大小。亦稱為初級球差係數。同理可得垂軸球差公式:
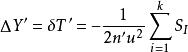 初級象差
初級象差初級彗差
對於初級子午彗差,需先求知子午面內上、下和主光線的像高Ya`,Yb`,Yz`,可寫為:
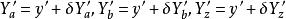 初級象差
初級象差將它們代入彗差計算公式,得:
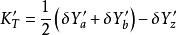 初級象差
初級象差上光線,其初始坐標為:y1、η1= ρ、ζ1= 0;下光線,其初始坐標為:y1、η1= -ρ、ζ1= 0;主光線,其初始坐標為:y1、η1 = ζ1 = 0,分別代入得:
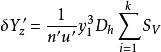 初級象差
初級象差代入並簡化,得初級子午彗差公式:
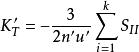 初級象差
初級象差用同樣的方法。得弧矢彗差公式:
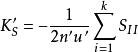 初級象差
初級象差並且,初級子午彗差是初級弧矢彗差的3倍。
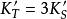 初級象差
初級象差初級像散和場曲
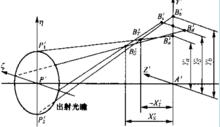
如圖所示,子午寬光束場曲可寫為:
 初級象差
初級象差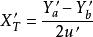 初級象差
初級象差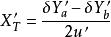 初級象差
初級象差改寫成:
代入並簡化得到寬光束初級場曲:
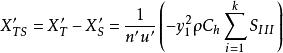 初級象差
初級象差令ρ →0,求細光束像散和場曲,有
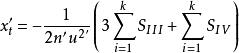 初級象差
初級象差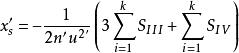 初級象差
初級象差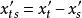 初級象差
初級象差由上面公式可知,xt`、xs` 決定於ΣS 和ΣS 。
欲達到初級像散和場曲同時消除,需ΣS和ΣS=0。
初級畸變
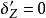 初級象差
初級象差畸變僅是主光線的像差,即主光線於高斯像面交點與理想像點間的偏離,並且弧矢分量,子午分量即為初級畸變,有:
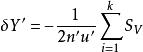 初級象差
初級象差第五塞德和數ΣS表征初級畸變。
