定義
凸多邊形(Convex Polygon)可以有以下三種定義:
 凸多邊形
凸多邊形沒有任何一個內角是優角(Reflexive Angle)的多邊形。
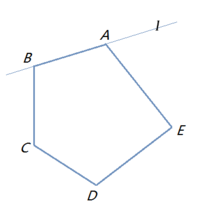
如果把一個多邊形的所有邊中,有一條邊向兩方無限延長成為一直線時,其他各邊都在此直線的同旁,那么這個多邊形就叫做凸多邊形。
凸多邊形是一個內部為凸集的簡單多邊形。簡單多邊形的下列性質與其凸性等價:1、所有內角小於等於180度。2、任意兩個頂點間的線段位於多邊形的內部或邊上。3、多邊形內任意兩個點,其連線全部在多邊形內部或邊上。
示例
所有的正多邊形都是凸多邊形。
所有的三角形都是凸多邊形。
性質
凸多邊形的內角均小於或等於180°,邊數為n(n屬於Z且n大於2)的凸多邊形內角和為(n-2)×180°,但任意凸多邊形外角和均為360°,並可通過反證法證明凸多邊形內角中銳角的個數不能多於3個。
凸多邊形所有對角線都在內部,邊數為n的凸多邊形對角線條數為2n(n-3),其中通過任一頂點可與其餘n-3個頂點連對角線。