簡介
在數學中，一個 凱勒流形（Kähler manifold）是具有滿足一個可積性條件的酉結構（一個U( n)-結構）的流形。特別地，它是一個黎曼流形、複流形以及辛流形，這三個結構兩兩相容。
這個三位一體結構對應於將酉群表示為一個交集：
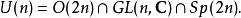凱勒結構 若沒有任何可積性條件，類似的概念是一個殆埃爾米特流形。如果辛結構是可積的（但復結構不要求），則這個概念是殆凱勒流形；如果復結構是可積的（但辛結構不要求），則為埃爾米特流形。
凱勒流形以數學家埃里希·凱勒命名，在代數幾何中占有重要的地位：它們是復代數簇的一個微分幾何推廣。
定義
帶有一個埃爾米特度量的流形是殆埃爾米特流形；凱勒流形是帶有滿足一個可積性條件的埃爾米特度量的流形，它有多種等價的表述。
凱勒流形可以多種方法刻畫：它們通常定義了具有一個附加結構的複流形（或具有附加結構的辛流形，或具有附加結構的黎曼流形）。
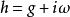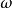凱勒結構 
凱勒結構 可以將這三個結構之間的聯繫總結為，這裡 h是埃爾米特形式， g是黎曼度量， i是殆復結構，而是殆辛結構。
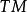凱勒結構 複流形 M上一個凱勒度量是切叢上一個埃爾米特度量，滿足一個有多種等價刻畫的條件（最幾何的方式是由度量誘導的平行移動在切空間上給出複線性映射）。利用局部坐標它規定如下：如果
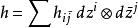凱勒結構 是埃爾米特度量，則伴隨的凱勒形式定義為（在差一個因子 i/2 的意義下）
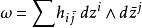凱勒結構 是閉的：即 dω = 0。如果 M帶有這樣一個度量則稱之為凱勒流形。
凱勒流形上的度量局部滿足
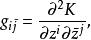凱勒結構 對某個函式 K，稱為凱勒勢。卡拉比率先考慮了凱勒流形上的微分幾何問題，特別是典則度量（包括凱勒-愛因斯坦，常數量曲率凱勒度量和極值度量）的存在性與唯一性問題。丘成桐於七十年代取得了突破性進展，近年來此問題取得了數學界極其廣泛的關注，屬於微分幾何中的中心問題之一。
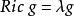凱勒結構 一個凱勒流形，伴隨的凱勒形式和度量叫做 凱勒-愛因斯坦（Kähler-Einstein，有時也叫愛因斯坦-凱勒）的若且唯若其里奇張量與度量張量成比例，，對某個常數 λ。這個名稱是為了紀念愛因斯坦關於宇宙常數的考慮。更多細節見愛因斯坦流形一文。
例子
復歐幾里得空間C帶著標準埃爾米特度量是一個凱勒流形。
環面C/Λ（Λ 為一完全格）由C上繼承一個平坦度量，從而是一個緊緻凱勒流形。
黎曼曲面上每個黎曼度量是凱勒的，因為ω閉的條件在（實）2 維是平凡的。
復射影空間CP有一個齊性凱勒度量，富比尼–施圖迪度量。向量空間C上一個埃爾米特形式定義了GL(n+1,C) 中一個酉子群；一個富比尼–施圖迪度量在差一個位似（整體縮放）的意義下由這樣一個 U(n+1) 作用下的不變性決定；由初等線性代數，任何兩個富比尼–施圖迪度量在CP的一個投影自同態下是等距的，故無需言明通常就說富比尼–施圖迪度量。
一個凱勒流形的複流形上的誘導度量是凱勒的。特別地，任何施坦流形（嵌入C）或代數簇（嵌入CP）是凱勒型的。這對它們的分析理論是基本的。
單位復球體B有一個凱勒度量叫做伯格曼度量，具有常全純截面曲率。
每個K3曲面是凱勒的（得自蕭蔭堂的一個定理）。
1.C
2.C
3.黎曼曲面上每個黎曼度量是凱勒的，因為ω閉的條件在（實）2 維是平凡的。
4.CP
5.C
6.B
7.每個K3曲面是凱勒的（得自蕭蔭堂的一個定理）。
凱勒流形的一個重要子類是卡拉比–丘流形。
相關條目
• 殆複流形
• 超凱勒流形（Hyper-Kähler manifold）
• 凱勒–愛因斯坦度量（Kähler–Einstein metric）
• Quaternion-Kähler manifold
• 復泊松流形
• 卡拉比–丘流形
