背景知識
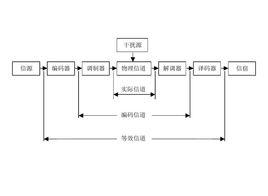
信道模型
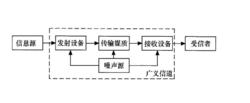 信道模型
信道模型在日常生活中,信息是指“訊息”,“情況”等。看電視、看報紙、看書、打電話、聽廣播、上網瀏覽,乃至聊天、開會,人們都獲得了“訊息”。訊息通過“訊息傳遞系統”傳遞,各種系統可以抽象為通訊系統模型。這一模型並不只限於通信系統,對於生物神經系統,遺傳系統,市場的經濟信號感知反饋系統,管理系統,都可以運用這個模型。在訊息傳遞系統中,其傳輸的是訊息;但訊息傳遞過程中,最普通,卻容易被忽視的一點是:收信人在收到訊息以前是不知道訊息的具體內容的。訊息的傳遞過程,對收信人來說,是一個從不知到知的過程,或者說是一個從不確定到確定的過程。
從通信過程來看,收信者的所謂“不知”就是不知道傳送端將傳送描述何種運動狀態的訊息。例如,看天氣預報前,不清楚天氣的將出現何種狀態;看天氣預報後,這種不確定性就大大縮小了。所以通信過程是一種從不確定到確定的過程。不確定性消除了,收信者就獲得了信息。所以香農認為, 信息是不定性的減少或消除。即
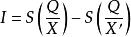 信道疑義度
信道疑義度I代表信息,Q 代表對某件事的疑問,S 代表不定性,X為收到訊息前關於Q的信息,X' 為收到訊息後關於Q 的信息。
不確定性
用數學的語言來講,不確定性就是隨機性,可以用機率論與隨機過程來測定不確定性大小。1948 年,香農發表了《通信的數學理論》,使用機率方法,奠定了現代資訊理論的基礎。離散情況下,信源的數學模型就是一個機率空間:
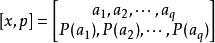 信道疑義度
信道疑義度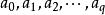 信道疑義度
信道疑義度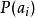 信道疑義度
信道疑義度 信道疑義度
信道疑義度 信道疑義度
信道疑義度事件已發生,則該事件所含有的自信息定義為:
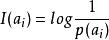 信道疑義度
信道疑義度 信道疑義度
信道疑義度 信道疑義度
信道疑義度 信道疑義度
信道疑義度 信道疑義度
信道疑義度 信道疑義度
信道疑義度代表兩種含義:當事件 發生以前,表示 發生的不確定性,當事件 發生以後,表示 所含有的信息量。即通訊前不確定性在狀態空間[X,P]中,通訊後,不確定性被縮小至狀態 ,信息量單位被定義為比特(bit):
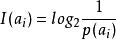 信道疑義度
信道疑義度信息熵
在物理學裡可以用“熵”的概念來描述某一種狀態自發變化的方向。比如把有規則排列的狀態稱為“低熵”,而混亂的狀態對應於“高熵”。而熵則是無序性的定量量度。熱力學第二定律的結論是:“一個孤立系統的熵永不減少”。換句話說,物質世界的狀態總是自發地轉變成無序,從“低熵”變到“高熵”。比如,當外力去除之後,整齊排列的分子就會自然地向紊亂的狀態轉變,而箱子左邊的煙一定會自發地向右邊擴散。這就是著名的“熵增定律”。
信息熵的定義與熵的定義相似,這裡說的信息熵一般是指資訊理論的香農理論。在訊息傳遞系統中,其傳輸的是訊息;但訊息傳遞過程中,最普通,卻容易被忽視的一點是:收信人在收到訊息以前是不知道訊息的具體內容的。訊息的傳遞過程,對收信人來說,是一個從不知到知的過程,或者說是一個從不確定到確定的過程。從通信過程來看,收信者的所謂“不知”就是不知道傳送端將傳送描述何種運動狀態的訊息。例如,看天氣預報前,不清楚天氣的將出現何種狀態;看天氣預報後,這種不確定性就大大縮小了。所以通信過程是一種從不確定到確定的過程。不確定性消除了,收信者就獲得了信息。所以香農認為, 信息是不定性的減少或消除。
信道的任務是以信號方傳輸和存貯信息,通過信息處理後,一般只會增加信息的損失,不可能增加原來獲得的信息。這意味著,在任何信息傳輸系統中,最後獲得的信息至多是信源所提供的信息;信息一旦丟失,如不觸及信源,就不能再恢復。這就是 信息不增原理,又稱數據處理定理,熵只是平均不確定性的描述,而不確定性的消除才是接受端獲得的信息量,信息量不應該與不確定性混為一談。
定義
信道疑義度也就是損失熵,指的是在輸出端收到輸出符號Y後,對於輸人端的符號X尚存在不確定性,即存在疑義 。對X尚存在的不確定性是由於干擾(噪聲)引起的,信道的這種特性稱為信道疑義度。它可用條件熵H(X|Y)來表征,即
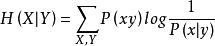 信道疑義度
信道疑義度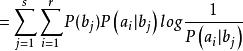 信道疑義度
信道疑義度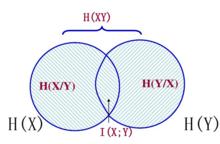 各類熵與平均互信息量關係
各類熵與平均互信息量關係此外,各類熵與平均互信息量關係可由右方維拉圖表示,用平均互信息量表示信道疑義度如下所示:
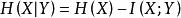 信道疑義度
信道疑義度推導
信道輸入信源X的熵H(X)是在接收到輸出Y以前,關於輸入變數X的先驗不確定性,稱為先驗熵。
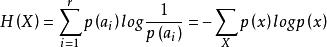 信道疑義度
信道疑義度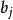 信道疑義度
信道疑義度接收到 後,關於X的不確定性為:
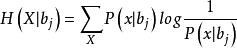 信道疑義度
信道疑義度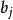 信道疑義度
信道疑義度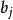 信道疑義度
信道疑義度這是接收到符號 後,關於X的後驗熵,後驗熵是當前信道接收端接收到輸出符號 後,關於輸入符號的信息測度。後驗熵在輸出符號Y的範圍內是個隨機量,對後驗熵在符號集Y內求數學期望得到條件熵——信道疑義度。
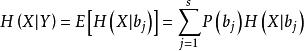 信道疑義度
信道疑義度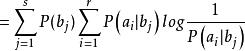 信道疑義度
信道疑義度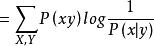 信道疑義度
信道疑義度物理意義
信道疑義度H(X|Y)也即為損失熵,它反映了信息受損失的情況,也間接反映了信道的功能屬性。需要注意的是H(X|Y)反映了信道兩端兩個隨機變數X和Y,由Y提取到得關於X的信息量,而並非損失的信息量。