概念
在一個n階 行列式D中,把元素 (i,j=1,2,.....n)所在的行與列划去後，剩下的(n-1)^2個元素按照原來的次序組成的一個n-1階行列式Mij,稱為元素 的 餘子式，Mij帶上符號(-1)^(i+j)稱為aij的代數餘子式,記作 A =(-1)^(i+j) M 。
通俗解釋
要得到最後結果的aij就劃掉原行列式的第i行第j列再把餘下的組成一個行列式算出來得到要求的aij
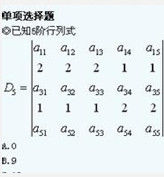代數餘子式代數餘子式代數餘子式
在一個n級行列式D中任意選定k行k列（k小於等於n）.位於這些行和列的焦點上的k*k個元素按照原來的次序組成的一個k級行列式M,稱為行列式D的一個k級子式.在D中划去這k行k列後餘下的元素按照原來的次序組成的n-k級行列式M'稱為k級子式M的餘子式。
基本信息
- 中文名：代數餘子式
- 屬於：數學術語
