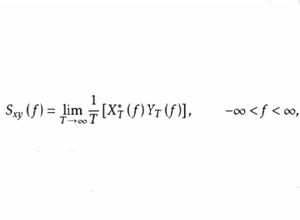互譜密度函式的定義
互譜密度函式的定義，數學上可描述為
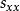互譜密度函式
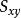互譜密度函式
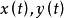互譜密度函式
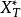互譜密度函式
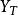互譜密度函式 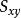互譜密度函式由於互譜密度函式的推導方法與自譜密度函式相同，它們的差別只是 是信號x(t)的自乘，而 是信號 與的互乘。應當注意的是，因為 與 一般不是互為共軛，所以 為複數性質。
互譜的單邊譜為
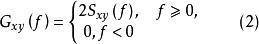互譜密度函式由式(2)互譜密度函式也可以描述為
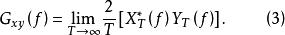互譜密度函式互譜密度函式的性質
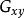互譜密度函式1． 的數學屬性
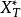互譜密度函式 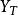互譜密度函式 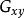互譜密度函式因為一般 與 是複數且不是互為共軛，所以 為複數性質。
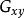互譜密度函式2． 的共軛變數交換性
證明：
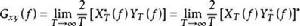互譜密度函式
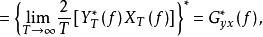互譜密度函式 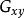互譜密度函式 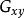互譜密度函式
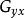互譜密度函式式中： 下標表示兩個測量信號的隨機變數x、y，該式表明， 數值上等於兩個信號x、y的信道互相交換後其應對的互譜密度函式 取共軛的結果。
3．互譜密度函式與互相關函式的關係
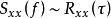互譜密度函式
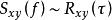互譜密度函式與 關係類似，可以得到 也是一個傅立葉變換對，即有
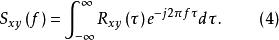互譜密度函式4．互譜密度函式的振幅和相位
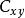互譜密度函式
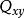互譜密度函式1)共譜密度函式 和重譜密度函式
由互譜密度函式與互相關函式的關係得
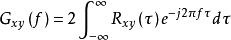互譜密度函式
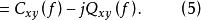互譜密度函式 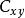互譜密度函式 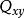互譜密度函式其中：共譜密度函式 為實部，重譜密度函式 為虛部。有
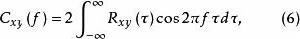互譜密度函式
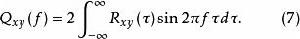互譜密度函式2)互譜密度函式的振幅和相位
由式(5)、式(6)和式(7)，可把互譜密度函式寫成複數表示式，有
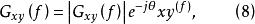互譜密度函式 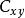互譜密度函式
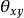互譜密度函式式中： 和 分別為互譜密度函式的振幅和相位，有
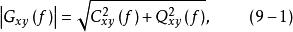互譜密度函式振幅：
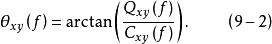互譜密度函式相位：
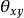互譜密度函式3)相位 的含義
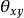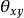互譜密度函式 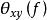互譜密度函式
互譜密度函式
互譜密度函式由時域中的時延將引起頻域中的相移，可推斷出 的含義： 為反映信號y(t)相對信號x(t)時延方面的信息， 為正，意味著在頻率 處信號y(t)落後於信號x(t)，反之亦然。
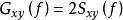互譜密度函式5． 的證明
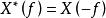互譜密度函式
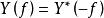互譜密度函式由傅立葉譜關於f=o軸共軛對稱的性質，有 和 ，將它們的左邊和右邊分別相乘後，得
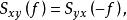互譜密度函式
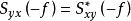互譜密度函式再將互譜密度函式的共軛變數交換性 代入上式，得
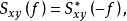互譜密度函式
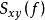互譜密度函式
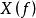互譜密度函式由此看出， 與 一樣，也具有關於f=0軸共軛對稱的性質。根據互譜密度函式的振幅為取摸概念，對於雙邊譜的振幅有
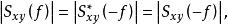互譜密度函式取摸後為關於f=0軸對稱，所以互譜的單邊譜可描述為
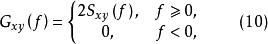互譜密度函式
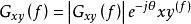互譜密度函式互譜的單邊譜為複數性質，也可描述為 。
